instagram

(Also available in WeScheme)

Students discover that in order for video game scores to change based on collisions, the computer needs to calculate the distance between two coordinates. This motivates exploration of the Pythagorean Theorem and its relationship to the distance formula.

Lesson Goals

Students will be able to:

  • Explain how the distance formula is related to the Pythagorean theorem.

  • Write a function for the distance formula.

Student-Facing Lesson Goals

  • Let’s investigate how the Pythagorean theorem can help us find the distance between two game characters.

  • Let’s write a function that takes in 2 points and returns the distance between them.

Materials

Supplemental Materials

Relevant Resources

  • This short video introduces viewers to the nearly 4000 year old Babylonian tablet known as Plimpton 322, which contains a table of Pythagorean Triples that long predates Pythagoras, as well as to Babylonians use of the base 60 system.

Key Points for the Facilitator

  • The distance formula is an excellent review of Circles of Evaluation. Have students work out the expression in small groups to foster discussion.

Preparation

  • This lesson includes a roleplay. In the roleplay students will move along a number line representing the x-axis in our game, which ranges from 0 to 640. Decide whether you will project, draw, or tape a number line on the board or floor.

  • Decide whether or not you plan to teach the option section on Finding the Hypotenuse of a Right Triangle. If you aren’t teaching the section and you are using our Google Slides, we suggest deleting the corresponding slides from the deck.

🔗What’s Missing from Our Game? 15 minutes

Overview

Students discover the need for distance calculation (first in one dimension, then in two) in video games.

Launch

  • Sign in to code.pyret.org (CPO), open your saved Game Starter File, and click "Run".

  • Take a minute to play with your games and think about what is left to do.

game image: astronaut and space craft on a landscape, with a right triangle showing the horizontal, vertical and diagonal distance between them

At this point:

  • The Target and Danger move on their own.

  • The Player responds to key-presses.

  • The Target and Danger reappear after they leave the screen.

It’s almost fully-playable!

If your students haven’t completed these other sections yet, make sure you leave time for them to do so! Here’s a link to a Sample Game with No Collision you can use if you’re demoing on the board.

  • What is missing from the game?

    • The characters aren’t doing anything when they collide and, as a result, the score isn’t changing!

  • What does it mean for characters to 'hit' one another? To collide?

    • The characters touch.

In the following activity, your students will role play two game characters moving across the screen. Draw or project a "number line" on the floor or across a wall of your classroom as the backdrop for the roleplay.

This number line represents the x-axis in our game. I need two volunteers to represent our DANGER and PLAYER and come find a spot to stand along it. Make sure to stand far enough apart that you’ll be able to take steps toward each other during the role play without touching.

Each image in the game is located based on its center, in the case of a human, our location would probably be given by our belly buttons. But the images in our game are much larger than their center points that locate them on the screen, so let’s have our DANGER and PLAYER hold their arms out like a T to represent the full width of the images they represent.

  • Are our characters currently colliding?

    • No.

  • How do you know?

    • They aren’t touching.

  • How will the computer know whether or not they are colliding?

    • We will have to teach it to check whether the coordinates of the characters are really close to each other.

  • What do you think would be the most straightforward way for us to program the computer to be able to determine that?

    • Find the distance between the characters.

  • How far apart are the DANGER and the PLAYER?

    • Answers will be roleplay-dependent.

  • How did you figure that out?

    • The goal is to illicit the response that students would subtract the smaller coordinate from the larger one (or subtract in any order and take the absolute value).

Let’s have our DANGER and TARGET each take a step toward each other.

  • How far apart are the DANGER and the PLAYER now?

    • Answers will be roleplay-dependent.

  • Are our characters colliding now?

    • No.

Let’s have our DANGER and TARGET switch places.

  • Are our characters colliding now?

    • No.

  • How far apart are the DANGER and the PLAYER?

    • Answers will be roleplay-dependent.

  • Did changing their positions change anything about how we calculated their distance?

    • Point out that students always subtract the smaller number from the larger one, regardless of the character order!

    • Distance is always positive.

Investigate

Our game computes 1-dimensional distance (vertical or horizontal) using a function called line-length. Let’s explore how it works!

Turn to the first section of Line Length Explore, find the definition of line-length in your game starter file and take a few minutes to record your Notices and Wonders with your partner.

  • What do you notice?

    • Answers will vary.

    • Both of the examples do the same thing, even though the numbers are given in a different order.

    • It’s a piecewise function!

    • It uses inequalities.

  • What do you wonder?

Complete Line Length Explore with your partner.

  • How does the way the line-length function works relate to how we calculated the distance between the characters in our role play?

    • The distance it calculates is always positive!

  • Why is the distance between two points always positive?

    • Because distance has nothing to do with direction. Route 66 is the same number of miles from Chicago to Los Angeles as it is from Los Angeles to Chicago.

We just practiced computing the distance in 1-dimension, which is useful if the Player and Danger have the same x- or y-coordinate. But how do we compute the distance between two points when both the x- and y-coordinates are different?

  • Scroll down to 4. Collisions in your game file and look for the distances-color definition.

  • Right now this value is defined to be the empty string "".

  • Change this to a color that will show up on your background and click "Run".

This setting draws lines from your Player to each of the other characters, and then uses those lines as the hypotenuse of right triangles! The legs of these triangles show the distance in 1 dimension each (on the x- and y-axis).

Here’s a link to a Sample Game with Distance Lines Made Visible to use if you’re demoing the instruction on the board.

  • What happens when we turn on distances-color?

    • There are right triangles that are constantly changing shape!

    • One right triangle connects the PLAYER and the DANGER.

    • Another right triangle connects the PLAYER and the TARGET.

  • How do these triangles relate to the distance between the PLAYER and the other characters?

    • The diagonal distance between two characters is represented by the hypotenuse of the right triangle that connects them.

    • The legs of the triangle represent the horizontal and vertical distances being calculated by line-length.

Our line-length function computes the horizontal and vertical distance between two characters, but in order to compute the diagonal distance between two characters in a video game, we’ll need a special formula that considers both the vertical and the horizontal distances between them!

Synthesize

Why do we care how far apart our game characters are?

🔗Finding the Hypotenuse of a Right Triangle optional

Overview

Students explore visual proofs of the Pythagorean Theorem as a foundation for understanding the distance formula.

Launch

Let’s take a few minutes to explore and respond to Exploring Proofs without Words (Desmos).

If you would like your students to do their summative reflection using paper-and-pencil, have them complete Proof Without Words in lieu of the final slide in the Desmos activity.

If you’d rather engage your students with these GeoGebra files as a whole class, use these links: proof 1, proof 2, proof 3, proof 4.

Investigate

As we saw in the GeoGebra activities, there is a special relationship between the area of the 3 squares that can be drawn using the 3 legs of a right triangle to determine the lengths of the sides:

The areas of the two smaller squares will add up to the area of the larger square.

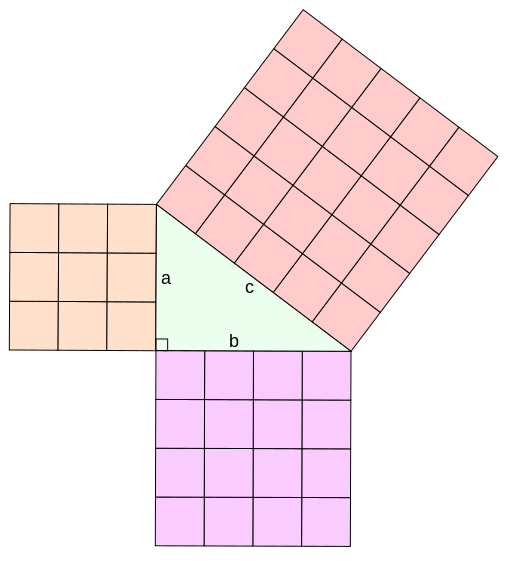
A right triangle with a square attached to each of its legs, such that the smallest leg (a) has an orange square composed of 9 square units, the longer leg (b) has a pink square composed of 16 square units, and the red square off the hypotenuse (c) is composed of 25 square units

A right triangle with a square attached to each of its legs, such that the smallest leg (a) has an orange square composed of 9 square units, the longer leg (b) has a pink square composed of 16 square units, and the red square off the hypotenuse (c) is composed of 25 square units

A right triangle with a square attached to each of its legs, such that the smallest leg (a) has an orange square composed of 9 square units, the longer leg (b) has a pink square composed of 16 square units, and the red square off the hypotenuse (c) is composed of 25 square units

If we label the two legs a and b and the hypotenuse c, as seen in the diagram, this rule, known as the Pythagorean Theorem can be described using the following equation:

a2 + b2 = c2

  • But how does the Pythagorean Theorem relate to distance in a video game?

    • If we think of any diagonal distance as the hypotenuse of a right triangle, the legs of the triangle correspond to the associated horizontal and vertical distances.

    • If we solve the Pythagorean Theorem for c instead of c2, it calculates diagonal distance based on horizontal and vertical distances!

c = √a2 + b2

two pyret characters located at (1,8) and (9,2) on a coordinate plane. They are connected by a right triangle whose legs are 6 units and 8 units and hypotenuse is labeled "how far apart?

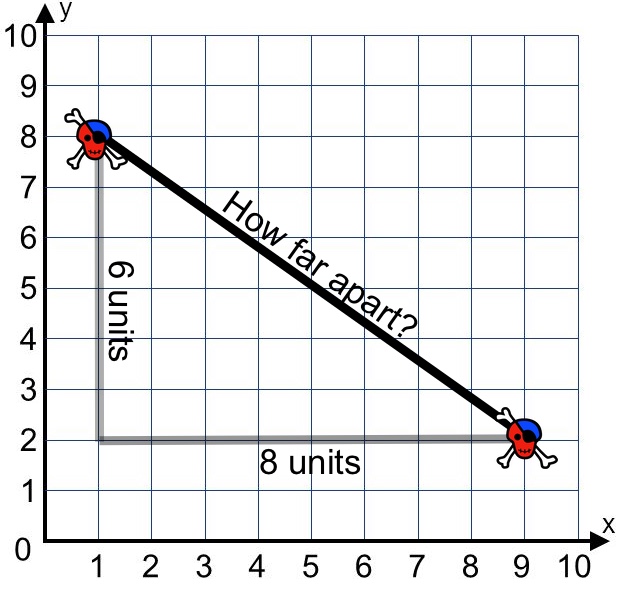
  • How could we use the equation to find the distance between these two pyret characters?

    • c = √82 + 62

    • c = √64 + 36

    • c = √100

    • c = 10

If you would like your students to do some Pythagorean Theorem Practice during this lesson, now would be a good time.

Pythagorean Theorem to video games

We recommend carving out 4.5 minutes and wowing your students with Tova Brown’s Video of a Geometric Proof of the Pythagorean Theorem and its application to finding distance between game characters. Then have them try explaining the proof to one another.

In our case, the lengths A and B are computed by the line-length function we already have!

Synthesize

  • The Pythagorean Theorem describes right triangles. Why is it also able to help us find distance?

🔗Diagonal Distance in Our Game 30 minutes

Overview

Students extend their understanding of distance from one dimension to two.

Launch

We know that we can use the Pythagorean Theorem to find the hypotenuse of a triangle from the lengths of its legs. And we know that there are hidden right triangles connecting the characters in our game. Now we have to figure out how to apply what we know in our game code.

  • If we had one player at (0,0) and another player at (4,3), we’d see a right triangle and the lengths of the legs would be 3 and 4.

A right triangle with legs of lengths 4 and 3 connects the points (0, 0) and (4,3).

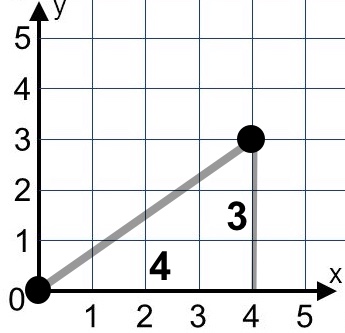
How would we use the Pythagorean Theorem to find the hypotenuse of the triangle?

  • We would add 32 and 42, or 9 and 16, to get 25. The square root of 25 is 5, so the length of the hypotenuse is 5.

On Writing Code to Calculate Missing Lengths we’ve provided screenshots from two games where the horizontal and vertical distances between the characters are shown. Students are asked to write the code to calculate the distance between these characters using the Pythagorean Theorem. You could also have them do the computations (using a calculator) and compare their results to what their code evaluates to.

Investigate

  • With your partner, complete the reading code section of Distance on the Coordinate Plane.

  • When you’re prepared to discuss how the line-length function is used in the code, see if you can figure out how to write the code for the second problem.

Why line-length?

Students learn early on that distance in 1-dimension is computed via | x2 - x1 |, and that distance is always a positive value. The Pythagorean Theorem teaches students that the length of the hypotenuse is computed based on the distance in the x- and y-dimension.

Most math textbooks, however, show the distance formula without connecting back to that theorem.

√(x2 - x1)2 + (y2 - y1)2

A student who asks whether it’s a problem when x2 - x1 is negative is displaying a deep understanding of what’s going on!

Using the line-length function explicitly connects the distance formula back to the 1-dimensional distance students know, allowing them to apply prior knowledge and better connect back to the Pythagorean Theorem itself.

This effectively rewrites the distance formula as:

√| x2 - x1 |2 + | y2 - y1 |2

  • What is line-length being used for in the code?

    • To compute the horizontal distance between the x-coordinates of the 2 characters.

    • To compute the vertical distance between the y-coordinates of the 2 characters.

For more practice writing code to generate the distance between two fixed points, have students complete Distance From Game Coordinates and Distance From Game Coordinates 2.

All of the distance work we’ve done so far has been focused on a screenshot of a moment in time.

With the game stopped in that moment, we knew either the exact location of our characters or the exact distances between them. But, as we play our games, the characters are constantly changing locations.

To calculate the distance between objects whose locations are constantly changing, we need to use variables!

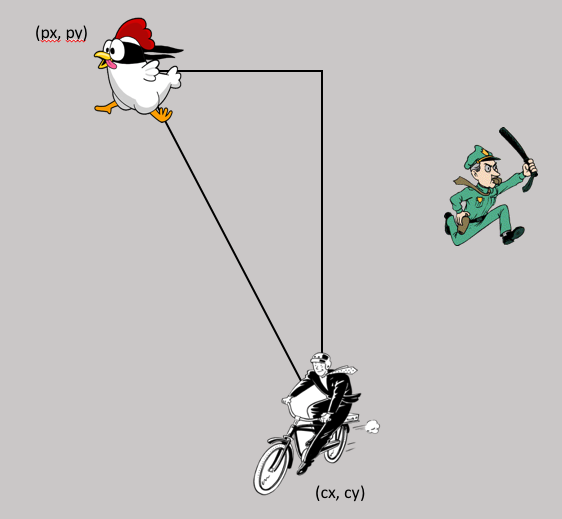  • Screenshot of a game where the Chicken (px,py) and the bicyclist (cx, cy) are connected by the hypotenuse of a right triangleTurn to Distance (px, py) to (cx, cy) and use the Design Recipe to help you write a function that takes in two coordinate pairs (four numbers) of two characters (px, py) and (cx, cy) and returns the distance between those two points.

  • HINT: The code you wrote in Circles of Evaluation: Distance between (0, 2) and (4, 5) can be used to give you your first example!

  • When you’re done, fix the broken distance function in your game file, click "Run" and check that the right triangles in your file now appear with reasonable distances for the hypotenuse.

Extension: Finding the length of the leg of a triangle

If we knew the lengths of the hypotenuse and one leg of the triangle, could we use the formula A2 + B2 = C2 to compute the length of the other leg?

Take a look at the two examples on Comparing Code: Finding Missing Distances.

  • There’s a subtle difference between the two examples! What is it?

    • In the first example, the length of the hypotenuse is missing. In the second example, the length of a leg is missing.

  • Can you explain why they need to be written differently?

    • Finding the hypotenuse requires finding the square root of the A2 + B2, whereas finding a leg requires finding the square root of the difference between C2 and B2.

Common Misconceptions

It is extremely common for students to put variables in the wrong order. In other words, their program looks like …​num-sqrt(num-sqr(line-length(x1,y1)) + num-sqr(line-length(x2, y2)))…​ instead of …​num-sqrt(num-sqr(line-length(x2 x1)) + num-sqr(line-length(y2 y1)))…​

In this situation, remind students to look back at what they circled and labeled in the example steps. This is why we label!

Synthesize

  • Where do you see one formula being used inside the other?

🔗Additional Exercises

  • Use the Design Recipe to solve Word Problem: line-length.

  • Modify line-length to make use of the absolute value function: num-abs.

These materials were developed partly through support of the National Science Foundation, (awards 1042210, 1535276, 1648684, 1738598, 2031479, and 1501927). CCbadge Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.

Lessons

    Aligns to: