Linear Regression

Students are introduced to the concept of linear regression, and learn how to interpret the slope and y-intercept. For teachers who have the need and the bandwidth to go deeper, this is a good opportunity to teach the algorithm behind linear regression.

Have students write down what they think, then quickly survey the class.

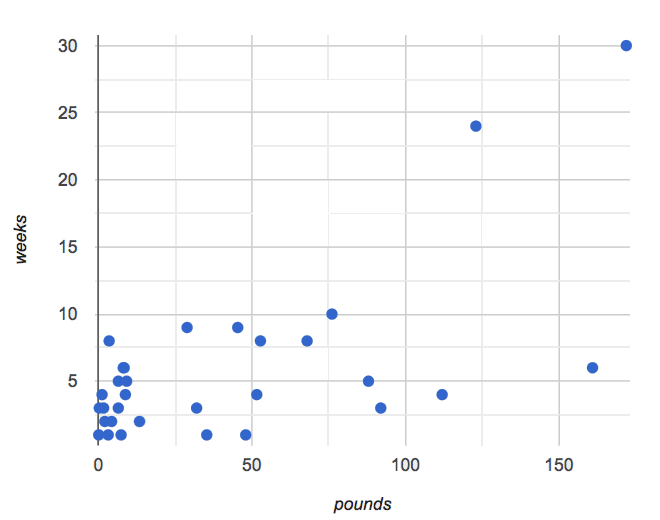🖼Show image We are asking if we can use an animal’s size or age to predict how long it will take to be adopted. A scatter plot of adoption time versus size does suggest that smaller animals get adopted faster than larger animals. Similarly, younger animals tend to be adopted faster than older ones.

Can we be more precise about this, and actually predict how long it will take an animal to be adopted, based on these factors? And which one would give us a better prediction?

The mean, median, and mode are three different ways to measure the “center” of a dataset in one dimension. Each represents a different way to collapse a bunch of points on a number line into a single, summary value. If the “center” of points on a one dimensional number line is a single point, what is the “center” of points in a two-dimensional cloud?

What we need to do is find a line — called a line of best fit, or a regression line — that is at the center of this cloud. Each point in our scatter plot “pulls” on the line, with points above the line yanking it up and points below the line dragging it down. Points that are really far away — especially influential observations that are far out in the x direction —- pull on the line with more force. This line can be graphed on top of the scatter plot as a function, called the predictor function.

Given a value on the x-axis, this line allows us to predict what the corresponding value on the y-axis might be. This allows us to make predictions based on our data.

Data scientists use a statistical method called linear regression to pinpoint linear relationships in a dataset. When we draw our regression line on a scatter plot, we can imagine a rubber bands stretching vertically between the line itself and each point in the plot — every point pulls the line a little “up” or “down”. Linear regression is the math behind the line of best fit.

Let’s explore scatter plots for weeks-v-pounds and weeks-v-age.

After looking at the point clouds, we are left with a few questions:

Give students some time to experiment, then share back observations. Can they come up with rules or suggestions for how to minimize error?

Students are introduced to the lr-plot function in Pyret, which performs a linear regression and plots the result.

Pyret includes a powerful display, which (1) draws a scatter plot, (2) draws the line of best fit, and (3) even displays the equation for that line:

🖼Show image lr-plot is a function that takes a Table and the names of 3 columns:

Our goal is to use values of the variable on our x-axis to predict values of the variable on our y-axis.

The resulting scatter plot looks like those we’ve seen before, but it has a few important additions. First, we can see the line of best fit drawn onto the plot. We can also see the equation for that line (in red). In this plot, we can see that the slope of the line is 0.792, which means that on average, each extra year of age results in an extra 0.792 weeks of waiting to be adopted (about 5 or 6 extra days). By plugging in an animal’s age for x, we can make a prediction about how many weeks it will take to be adopted. For example, we predict a 5-year-old animal to be adopted in 0.7925 + 2.285 = 6.245$\displaystyle 0.792(5) + 2.285 = 6.245$ weeks. That’s the y-value exactly on the line at x=5.

The intercept is 2.285. This is where the best-fitting line crosses the y-axis. We want to be careful not to interpret this too literally, and say that a newborn animal would be adopted in 2.285 weeks, because none of the animals in our dataset was that young. Still, the regression line (or line of best fit) suggests that a baby animal, whose age is close to 0, would take only about 3 weeks to be adopted.

We also see the r$\displaystyle r$-value is +0.442. The sign is positive, consistent with the fact that the scatter plot point cloud and line of best fit, slope upward. The fact that the r$\displaystyle r$-value is close to 0.5 tells us that the strength is moderate. This makes sense: the scatter plot points are somewhere between being really tightly clustered and really loosely scattered.

A predictor only makes sense within the range of the data that was used to generate it.

Toddlers grow a lot faster than adults. A regression line predicting the height of toddlers based on age would predict that a 60-year-old is 10 feet tall!

Statistical models are just proxies for the real world, drawn from a limited sample of data: they might make a useful prediction in the range of that data, but once we try to extrapolate beyond that data we may quickly get into trouble!

Students learn how to write about the results of a linear regression, using proper statistical terminology and thinking through the many ways this language can be misused.

How well can you interpret the results of a linear regression analysis? How would you explain it to someone else?

Let’s take a look at how the Data Cycle can be used with Linear Regression, and how the result can be used to form our Data Story.

Have students explain the connection between the Ask Questions and Consider Data step. Do they match? Why or why not?

At the bottom of the page we have the Data Story for this question, which includes the results of the analysis and a responsible way to write about them. When looking at a regression for adoption time v. age for just the cats, we saw that the slope of the predictor function was +0.23, meaning that for every year older, we expect a cat to take +0.23-weeks longer to be adopted. The r$\displaystyle r$-value was +0.566, confirming that the correlation is positive and indicating moderate strength.

Have students read their data stories aloud, to get comfortable with the phrasing.

Students repeat the previous activity, this time applying it to their own dataset and interpreting their own results. Note: this activity can be done briefly as a homework assignment, but we recommend giving students an additional class period to work on this.

Now that you’ve gotten some practice performing linear regression on the Animals Dataset, it’s time to apply that knowledge to your own data!

Have students share their findings with the class. Get excited about the connections they are making and the conclusions they are drawing! Encourage students to make suggestions to one another about further analysis.

🖼Show image

The word “linear” in “linear regression” is important here. In the image on the right, there’s clearly a pattern, but it doesn’t look like a straight line!

There are many other kinds of statistical models out there, but all of them work the same way: use a particular kind of mathematical function (linear or otherwise), to figure out how to get the “best fit” for a cloud of data.