(Also available in CODAP)
Students explore the concept of "shape", using histograms to determine whether a dataset has skewness, and what the direction of the skewness means. They apply this knowledge to the Animals Dataset, and then to their own.
Lesson Goals |
Students will be able to…
|
Student-facing Lesson Goals |
|
Materials |
|
🔗Describing Shape 30 minutes
Overview
This activity focuses on describing shape based on a histogram. Students learn about "left skewed", "right skewed", and "symmetric" data, and what those descriptions tell us about a dataset.
Launch
Shape is one way to quickly describe what values are more or less common in a dataset. Some might occur very frequently, while others are rare. That information can be gathered from a distribution of data: any representation of the data that shows the frequency of each value (like a table, list, or chart!).
Distributions can show where data points are clustered together or spread thin. Data Scientists spend a lot of time looking at data displays to examine their shape, because the numbers don’t tell the whole story!
In fact, you lose a lot of insight into your dataset if you don’t look at the shape. The Datasaurus Dozen are a wonderful collection of dissimilar graphics whose summary statistics are identical.
Histograms create fixed-size bins, which contain varying numbers of data points.
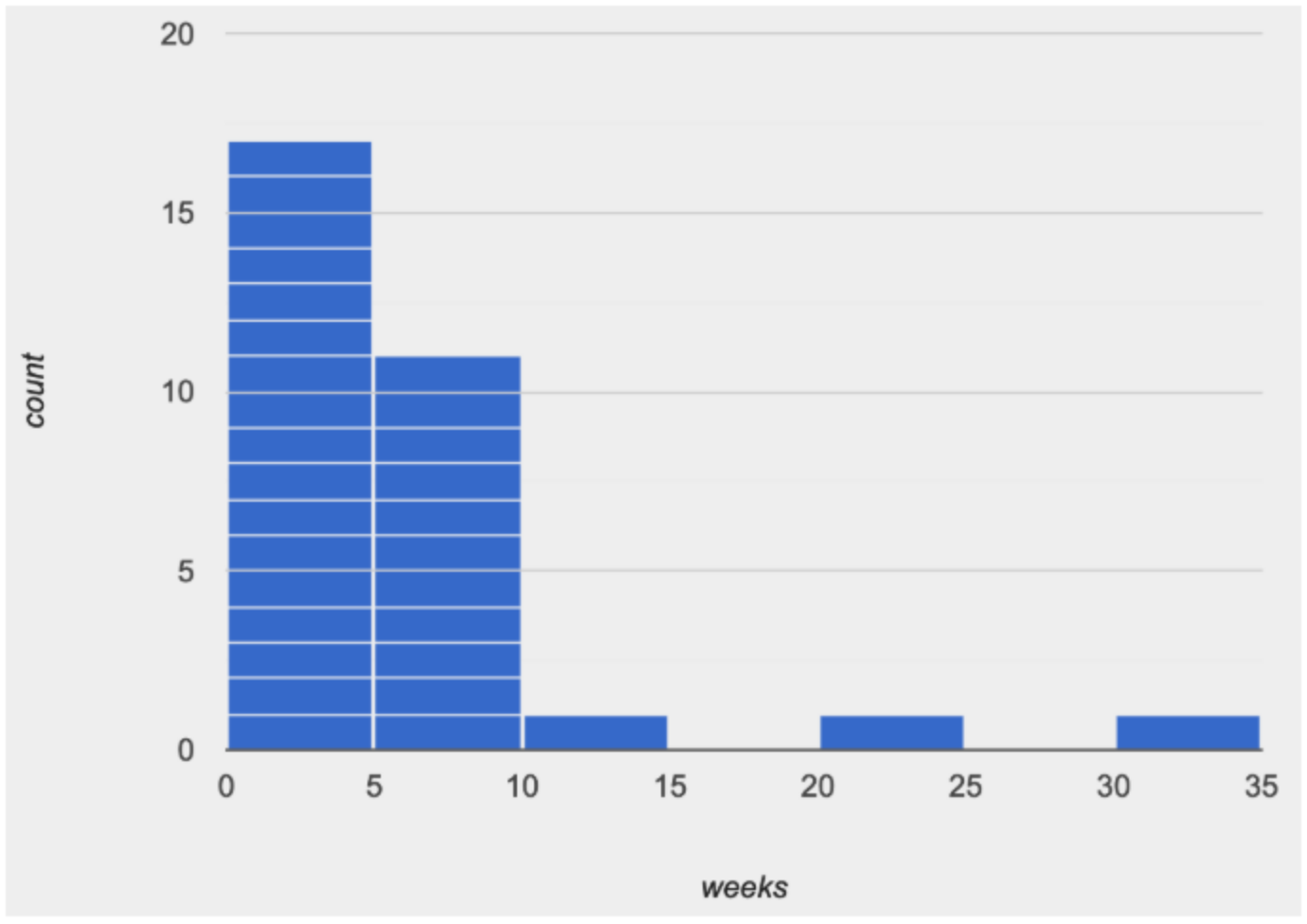 We can think of the data being "stacked" in these fixed bins, like jeans in a store separated by size: one stack for Small, another for Medium, and so on.
We can think of the data being "stacked" in these fixed bins, like jeans in a store separated by size: one stack for Small, another for Medium, and so on.
The height of a histogram bar tells us how much data falls within that interval. Taller stacks have more data points than short ones.
Look at the image on the right: most of the data is clustered on the left side, and there are a few unusually high values way off to the right. But how do we describe this shape, and what does it mean?
Let’s look at some real-world examples of the most common shapes:
1. Skewed right, or high outliers
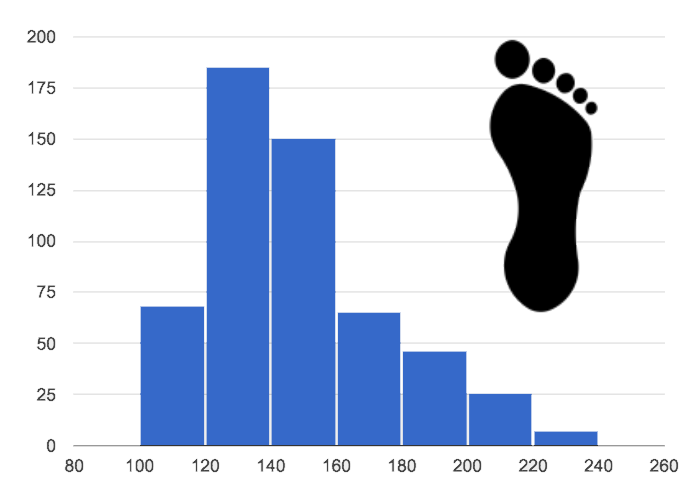 Most points are clumped around what’s typical, but they trail off to the right with a few unusually high values (or outliers). We see this shape often in the real world.
Most points are clumped around what’s typical, but they trail off to the right with a few unusually high values (or outliers). We see this shape often in the real world.
-
The average US woman gives birth around age 26, but some do even after 45! No one is giving birth at age 7 to balance this out, so the outliers are all on the right.
-
Personal income almost always shows right skewness or high outliers. There are usually a few billionaires that are far above average, and aren’t balanced out by any earners that are equally far below average.
A skew-right distribution looks like the toes on your right foot!
2. Skewed left, or low outliers
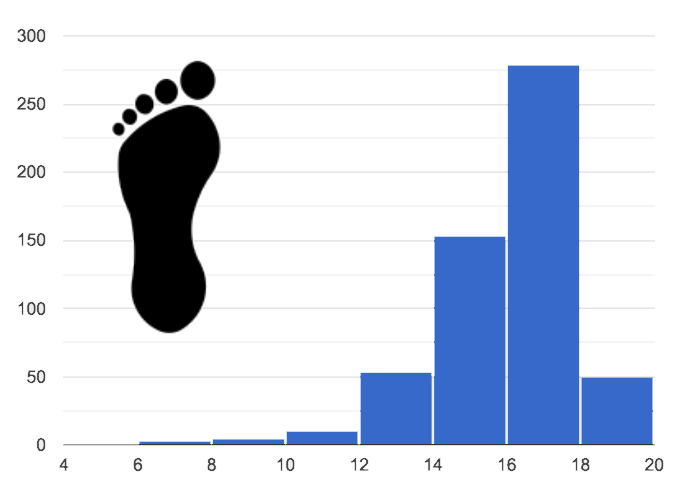 Values are clumped around what’s typical, but they trail off to the left with a few unusually low values (or outliers).
Values are clumped around what’s typical, but they trail off to the left with a few unusually low values (or outliers).
-
Most adults have close to a full set of 32 teeth, but a few hockey players might have a very small number of teeth. Since no one has 10 extra teeth to balance this out, the only outliers are on the left.
-
A school cafeteria mostly buys canned goods in huge sizes, but might have a few ingredients in smaller sizes. If we looked at the ounces per can we’d see a shape that has left skewness and/or low outliers.
A skew-left distribution will look like the toes on your left foot!
3. Symmetric: values are balanced on either side of the middle.
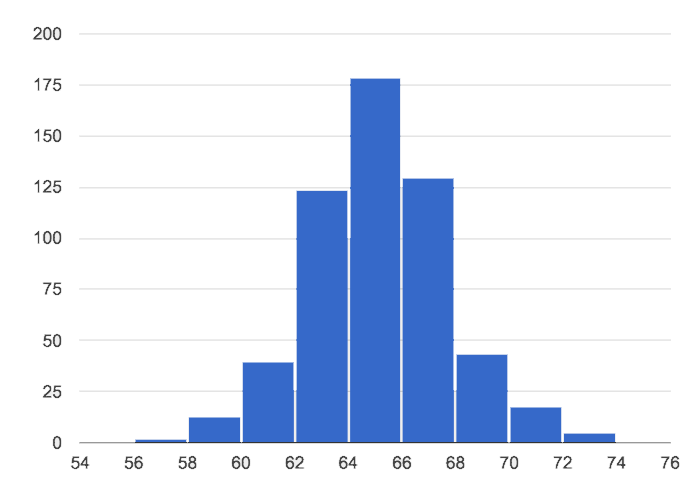 In a symmetric distribution, it’s just as likely for the variable to take a value a certain distance below the middle as it is to take a value that same distance above the middle. Examples:
In a symmetric distribution, it’s just as likely for the variable to take a value a certain distance below the middle as it is to take a value that same distance above the middle. Examples:
-
It’s just as likely for a newborn baby to be a certain number of ounces below average weight as it is to be that number of ounces above average weight.
-
At many restaurants, the busiest dinner time is around 7pm. But there are always a few people who want to eat earlier or later.
For those in an AP Stats class or full-year Data Science class, you may wish to include a discussion of other kinds of distributions (e.g. - normal/gaussian, unimodal, bimodal, etc..)
Investigate
-
Make a histogram for the pounds column in the animals table, sorting the animals into 20-pound bins.
-
Students should enter the code:
histogram(animals-table, "name", "pounds", 20)
-
-
Would you describe the shape of your histogram as being skewed left, skewed right, or symmetric?
-
The histogram is skewed left.
-
-
Which one of these statements is justified by the histogram’s shape: (1) A few of the animals were unusually light, (2) A few of the animals were unusually heavy, or (3) It was just as likely for an animal to be a certain amount below or above average weight.
-
The 2nd statement "a few of the animals were unusually heavy" is the only one that applies, given the histogram’s shape.
-
-
Try bins of 1-pound intervals, then 100-pound intervals. Which of these three histograms best satisfies our rule of thumb?
-
Our rule of thumb is that a histogram should have between 5–10 bins. The first histogram we made - with 20-pound bins - had a total of ten bins, so it best satisfies our rule.
-
-
On Identifying Shape - Histograms, describe the shape of the histograms you see there.
-
On Data Cycle: Shape of the Animals Dataset, describe the pounds histogram and another one you make yourself. When writing down what you notice, try to use the language Data Scientists use, discussing both skew and outliers.
Outliers… do they stay or do they go?
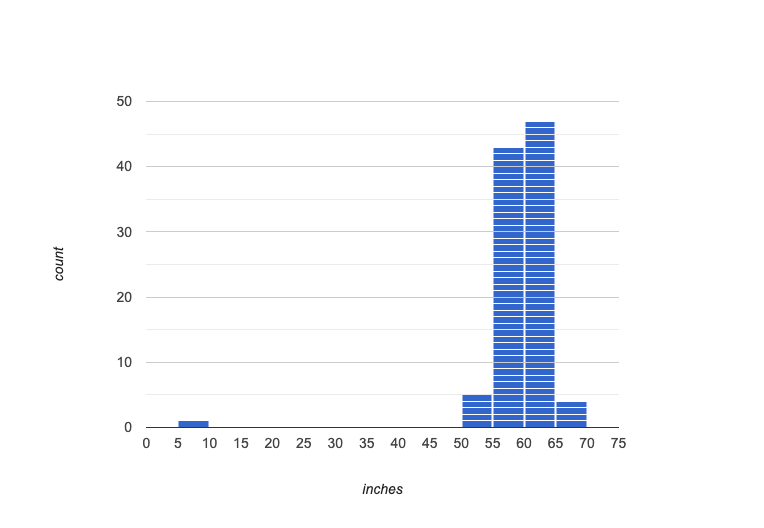 Suppose we survey the heights of 12 year olds, and almost all values are clustered between 50-70in. There’s a very low outlier, however, at 6in.
Suppose we survey the heights of 12 year olds, and almost all values are clustered between 50-70in. There’s a very low outlier, however, at 6in.
-
Is there really a 12 year old who is 6 inches tall?
-
Probably not! This could very well be a typo (maybe someone meant to type "60" instead of "6"?).
-
"Junk" data is harmful, because it can drastically change your results!
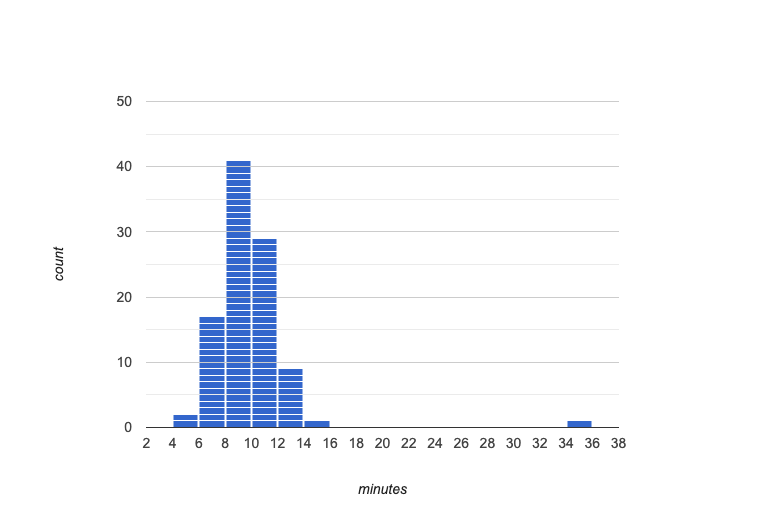 Suppose we survey the number of minutes it takes for fans to find their seats at a stadium, and almost all values are clustered between 4-16 minutes. There’s a very high outlier, however, at 35 minutes.
Suppose we survey the number of minutes it takes for fans to find their seats at a stadium, and almost all values are clustered between 4-16 minutes. There’s a very high outlier, however, at 35 minutes.
-
Did it really take someone 35 minutes to find their seat?
-
It’s very possible! Maybe it’s someone who takes a long time getting up stairs, or someone who had to go far out of their way to use the wheelchair ramp!
-
An outlier can also could be a really important part of your analysis!
As a data scientist, an outlier is always a reason to look closer. And whether you decide to keep or remove it from your dataset, make sure you explain your reasons in your write-up!
With your partner, complete Outliers: Should they Stay or Should they Go?.
What Shape Makes Sense?
If time allows, here’s a great way to get students walking around and thinking more deeply about distributions!
Using flip-chart paper or whiteboard space, designate poster-sized regions around the classroom titled "Symmetric", "Skew Left", and "Skew Right". You may want to have 2-3 of each, depending on the number of students and size of the classroom. Divide the class into teams, such that each group takes a region of the room.
Each team looks at the region they’re in front of, and must (a) draw a histogram with that shape and (b) brainstorm a sample that would likely result in that distribution. Once each team has completed the task, the teams rotate to the next poster and brainstorm another sample. They complete this until every team has come up with at least one unique example for symmetric, skew left, and skew right distributions.
Synthesize
-
For which distributions was it easiest to come up with an example?
-
For which distributions was it hardest to come up with an example?
Histograms are a powerful way to display a dataset and see its shape. But shape is just one of three key aspects that tell us what’s going on with a quantitative column of a dataset. We will also want to learn about center and spread!
🔗Data Exploration Project (Visualizing Shape) flexible
Overview
Students apply what they have learned about visualizing shape to the histograms they have created for their chosen dataset. They will add to their Data Exploration Project Slide Template a more detailed interpretation of their histograms using new vocabulary.
Visit Project: Dataset Exploration to learn more about the sequence and scope. Teachers with time and interest can build on the exploration by inviting students to take a deep dive into the questions they develop with our Project: Research Capstone.
Launch
Let’s review what we have learned about visualizing the shape of data.
-
Describe a histogram that is skewed right. Are its outliers high or low?
-
Values are clumped around what’s typical, with low outliers.
-
-
Describe a histogram that is skewed left. Are its outliers high or low?
-
Values are clumped around what’s typical, with high outliers.
-
-
Describe a histogram that is symmetric.
-
It’s just as likely for the variable to take a value a certain distance below the middle as it is to take a value that same distance above the middle.
-
Investigate
Let’s connect what we know about visualizing the shape of the data to the histograms we created for your chosen dataset.
-
Open your chosen dataset starter file in Pyret.
-
For this analysis, you’ll want to look at the Data Cycle that you completed during the Histograms lesson.
-
Recreate the histograms that you made before. Now, edit and expand your discussion so that it uses the new vocabulary that you’ve used.
If your students who need a fresh copy of the Data Cycle template, distribute @opt-printable{data-cycle-quantitative.adoc}.
It’s time to add to your Data Exploration Project Slide Template.
-
For each of the histograms that you have added, edit and / or expand upon the interpretations you provided during the Histograms lesson.
-
Be sure to integrate the new vocabulary we have learned, including: shape, skewed left, skewed right, and symmetric.
-
Describe what this shape tells you about the quantitative column you chose.
Synthesize
Have students share their findings.
-
What shapes did you notice in your histograms?
-
Did you discover anything surprising or interesting about your dataset?
-
Were there any surprises when you compared your findings with other students?
These materials were developed partly through support of the National Science Foundation, (awards 1042210, 1535276, 1648684, 1738598, 2031479, and 1501927).  Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
