instagram
Lessons

    Aligns to:

    (Also available in CODAP)

    Students are introduced to mean, median and mode(s) and consider which of these measures of center best describes various quantitative data.

    Lesson Goals

    Students will be able to…​

    • Students explore the concept of center of a distribution, learning how to compute the mean, median and mode(s) of a dataset

    • Students find the mean, median and mode(s) of various columns in the Animals table

    Student-facing Lesson Goals

    • Let’s use mean, median, and modes to describe our data.

    Materials

    Supplemental Materials

    Preparation

    • The kinesthetic activity in this lesson requires a ruler and 4-8 pennies for each group of 3.

    • There is an optional activity in this lesson that would require you to print an extra data cycle for your students.

    • In each of the first 3 Investigate sections of this lesson, students will calculate a Measure of Center from a list. If you would like to be able to direct students to printed versions with space for them to write, make copies of Mean, Median, Mode(s) Practice.

    • If you are using our Google Slides, adjust them based on which of these activities you will be doing with your students.

    🔗Mean 15 minutes

    Overview

    Students learn about mean (or "average") as one way (among others!) to summarize a quantitative column, and how to compute it using Pyret.

    Launch

    One of the ways that Data Scientists summarize quantitative data is by talking about its center - literally asking "what is a typical value in this sample?", in the hopes of inferring something about a larger population.

    But there are many different ways to define "center", and each method has strengths and weaknesses. The shape of the data can play a huge role in whether or not one kind of summary is appropriate!

    Let’s take a moment to consider what values might be typical for the weight of our animals by completing What Value is Typical?.

    number line with dots above the line representing the weight of each of the animals. There is a big cluster between 0 and 17, a small cluster in the 30s and another small cluster in the 40s and individual dots spread out along the number line til a little above 120.

    • Do you think there is a midpoint of this sample?

      • There are 32 animals - meaning that there is not one point in the middle.

    • Is there a value that shows up most often in this sample?

      • Since we see that dots are stacked up, it seems likely that there is some repetition in the animals' weights.

    • What value did you decide was typical? Why?

      • There isn’t one right answer here! The point is for students to hear each other’s thinking, recognize that it’s hard to summarize the data with a single number, and understand that there are different logical frameworks for doing so.

    Each of these are different ways of “measuring center”.

    Investigate

    The Animal Shelter Bureau used a method of summary, called the mean, or "average" to report about the typical weight of pets, claiming that a typical animal weighs 40 pounds.

    • What do you already know about averages?

      • Sample Answer: To find the mean of a dataset we add all of the values and then divide their sum by the number of values in the dataset.

      • The mean is the number that "balances" all the other numbers in the sample.

    The Mean section of Mean, Median, Mode(s) Practice includes a printed version of the upcoming list.

    • We are going to learn to let Pyret compute the mean for us, but let’s first make sure we understand what we’re asking Pyret to do! How would we find the mean weight of five animals who weigh 17, 25, 23, 23 and 22 pounds?

      • First add 17 + 25 + 23 + 23 + 22 = 110 and then divide 110 ÷ 5 = 27

    If you have time, we recommend deepening your students' understanding by engaging them with the kinesthetic activity: Finding the Value of the Balancing Point!

    Kinesthetic Activity - Finding the Value of the Balancing Point

    The arithmetic mean is the number that "balances" all the other numbers in the sample. So let’s do some real balancing!

    Divide the class into groups of three. Supply each group with a ruler and 4-8 pennies. Make sure every group has at least one pen or pencil.

    1. The ruler represents a number line with values (weight) distributed equally across the line. If there’s values at every inch from 0 to 12, where should the pencil be placed in order to balance the ruler on top of it?

    2. Place a penny at 1 and 11. Where must the pencil be placed to balance those two values? What is the mean of the values [1, 11]?

    3. Place pennies at 1, 9 and 11. Where must the pencil be placed to balance those two values? What is the mean of of the values [1, 9, 11]?

    4. Suppose you were to place two pennies at 2, and a third penny at 8. Can you predict where the pencil should be placed?

    Pyret has a function that will compute the mean — or average — of any quantitative column in a Table.

    # mean :: Table, String -> Number

    Let’s test it out!

    • How did your calculation compare to the Animal Shelter Bureau’s claim that the average pet weighs nearly 40 pounds?

      • 39.715625 is very close to 40!

    • When might it be useful to know the average weight of the animals? Answers will vary.

      • If we were transporting them to a different shelter, knowing the average weight might help us confirm that a truck, boat or plane could support their collective weight.

    • When might it be risky to describe the weight of these animals using the average? Answers will vary.

      • If one of them were sick and we wanted to give it medicine, basing the dosage on the average would likely be way too little medicine for a big animal or a dangerously large amount of medicine for a little animal.

    Possible Misconceptions

    Just because a column contains numbers doesn’t mean the data is quantitative. We could sum and divide a collection of zip codes, for example, but the output wouldn’t correspond to some “center” zip code.

    Synthesize

    If you heard that the mean age of students in a kindergarten class was 21, would you be surprised? Why or why not?

    🔗Median 15 minutes

    Overview

    Students learn the algorithm and code for a second measure of center: the median and consider situations where taking the median is more appropriate than the mean.

    Launch

    You computed the mean of that column to be almost exactly 40 pounds. That IS the average…​

    …​but if we scan the dataset we’ll quickly see that most of the animals weigh less than 40 pounds. In fact, more than half of the animals weigh less than just 15 pounds.

    Why is the average so high? Kujo and Mr. Peanutbutter!

    The mean is being thrown off by a few extreme data points, called outliers because they fall far outside of the rest of the dataset. The mean may also be thrown off by the presence of skewness: a lopsided shape due to values trailing off to the left or right.

    There is another measure of center we can use called the median. Instead of averaging the data points, it identifies the “middle” value, which half of the values are smaller than and the other half are larger than.

    The algorithm for finding the median of a quantitative column is:

    1. Sort the numbers

    2. Cross out the highest and lowest number

    3. Repeat until there is only one number left…​

    4. When there are an even number of numbers in the list, as in the example below, there will be two numbers left at the end. Take the mean of those two numbers.

    Consider this list of ages: 25, 26, 28, 28, 28, 29, 29, 30, 30, 31, 32

    Here 29 is the median. It’s the middle number of the list and it separates the "bottom half” (5 values below it) from the "top half” (5 values above it).

    Now consider this list of ages: 3, 7, 9, 21

    There is no middle number. So the median of this list will be the mean of the two middle numbers, 7 and 9, which is 8.

    7 + 9 = 16 𝑎𝑛𝑑 16 ÷ 2 = 8

    The Median section of Mean, Median, Mode(s) Practice includes a printed version of the upcoming list.

    Find the median value of each of these two lists:

    • The median of 11, 3, 7 ,4, 5 is…​

      • 5 because it’s the middle value of 3, 4, 5, 7, 11.

    • The median of 11, 3, 7, 4 is…​

      • 5.5 because it’s the mean of 4 and 7, which are the middle values in the ordered list 3, 4, 7, 11

    Investigate

    Turn back to Summarizing Columns with Measures of Center and use the provided code to compute and record the median for the pounds column in the Animals Dataset.

    • How do the mean and median compare?

      • The median (11.3) is very different from the mean (39.7)!

    • Here we see the median (red) and mean (blue). 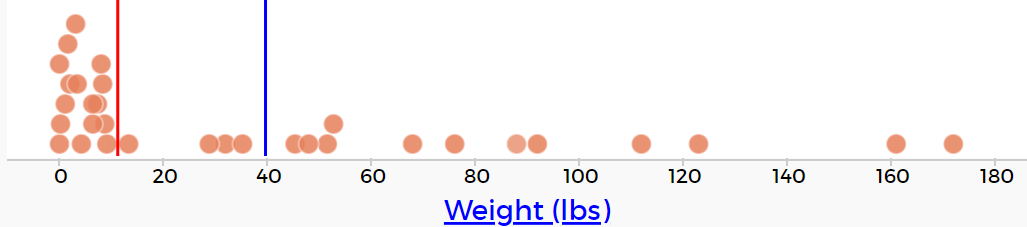number line with dots above the line representing the weight of each of the animals. There is a big cluster between 0 and 17, a small cluster in the 30s and another small cluster in the 40s and individual dots spread out along the number line til a little above 120. Which do you think better represents the data?

      • The median, because over half of the data is clustered quite close to it and the rest of the data is dispersed across a huge range. Very few animals have a weight close to 39.7.

    • If the median were much higher than the mean, what would we expect to be true about the distribution of the dataset?

      • The dataset is skewed left or has some very low outliers.

    The mean is a useful calculation when all of the points are fairly balanced on either side of the middle, but it distorts things for datasets with imbalance and extreme outliers.
    For skewed datasets, the median is a better summary.

    Synthesize

    Mean is generally the best measure of center, because it includes information from every single point. But it’s misleading for highly-skewed datasets, so statisticians fall back to the median.

    • Why would looking at the histogram for a dataset help us to decide whether mean or median would be a better measure of center?

      • Median is less sensitive to skew than mean, so seeing the shape will determine whether there’s a need for median over mean.

    • When there’s a strong left skew, will the mean be less than or greater than the median?

      • Less: the left skew pulls the mean to lower values.

    🔗Mode(s) 10 minutes

    Overview

    Students learn about the mode(s) of a dataset, how to compute them, and when it is appropriate to use them as a measure of center.

    Note: Mode(s) are often used to describe categorical data. Since Pyret can currently only calculate mode(s) from quantitative columns, we won’t be discussing that in this lesson…​ keep your ears peeled for news of an update next year!

    Launch

    The third measure of center is called the mode(s) of a dataset. The mode(s) of a dataset are the values that appear most often.

    Median and Mean always produce one number and many datasets are what we call “unimodal”, having just one mode. But sometimes there are exceptions!

    • If two or more values are equally common, there can be more than one mode.

    • If all values are equally common, then there is no mode at all!

    Consider the following three datasets:

    1, 2, 3, 4
1, 2, 2, 3, 4
1, 1, 2, 3, 4, 4

    • The first dataset has no mode at all!

    • The mode of the second dataset is 2, since 2 appears more than any other number.

    • The modes (plural!) of the last dataset are 1 and 4, because 1 and 4 both appear more often than any other element, and because they appear equally often.

    The Modes section of Mean, Median, Mode(s) Practice includes a printed version of the upcoming list.

    Take a minute to identify the mode(s) for each of the following datasets:

    • 11, 3, 7, 4, 5

    • 5, 7, 11, 11, 7, 7

    • 2, 3, 5, 4, 3, 7, 4

    Pyret has a function that will compute the modes of any quantitative column in a Table.

    # modes :: Table, String -> List

    Note: List is a new data type!

    Let’s test it out!

    Investigate

    • Turn to Summarizing Columns with Measures of Center and use the code provided to compute and record the modes of the pounds column.

    • Then complete the remaining questions in the Summarizing the Pounds Column section.

    • What did you learn from calculating the mode(s)?

      • The most common animal weights are 0.1 and 6.5! That’s well below our mean and even our median, which is further evidence of outliers or skewness.

    • Can we find the mean, median and mode(s) for any column?

      • No! We can only calculate Measures of Center for quantitative columns.

      • Note: Not all columns that contain numbers are quantitative! Taking the average of a list of zip codes doesn’t tell us anything at all!

    Synthesize

    • What must be true about a dataset for the mode(s) to do a good job of describing what is typical?

    • What can we learn from the modes of a dataset?

    🔗The Risk of Summarizing Data with a Single Number 15 minutes

    Overview

    Students consider the complexity of summarizing with a single number and learn how to decide which measure of center to use when. They then choose a column, compute all of its measures of center in Pyret, and interpret the results. Finally, they practice computing measures of center for a small dataset by hand and use their findings to critique misleading statements.

    Launch

    Summarizing a big dataset means that some information gets lost, so it’s important to pick an appropriate summary. Picking the wrong summary can have serious implications!

    Here are just a few examples of summary data being used for important things:

    • Students are sometimes summarized by two numbers — their GPA and SAT scores — which can impact where they go to college or how much financial aid they get.

    • Schools are sometimes summarized by a few numbers — student pass rates and attendance, for example — which can determine whether or not a school gets shut down.

    • Adults are often summarized by a single number — like their credit score — which determines their ability to get a job or a home loan.

    • When buying uniforms for a sports team, a coach might look for the most common size that the players wear.

    What other examples can you think of where a number or two are used to summarize something complex?

    Investigate

    You now have three different ways to measure center in a dataset. Every kind of summary has situations in which it does a good job of reporting what’s typical, and others where it doesn’t really do justice to the data.

    But how do you know which one to use? Depending on the shape of the dataset, a measure could be really useful or totally misleading!

    • "In 2003, the average American family earned $43,000 a year — well above the poverty line! Therefore, very few Americans were living in poverty."

    • Do you trust this statement? Why or why not?

      • Sample response: The mean is sensitive to outliers, and billionaires like Elon Musk, Jeff Bezos, etc. pull the mean heavily to the right. This makes it appear that the "average" American family earns far more than they actually do. That’s why the conclusion "very few Americans were living in poverty" cannot be drawn based on the mean.

    • Given the extreme income inequality in the United States, what measure of center would best represent a typical family income?

      • The median

    Consider how many policies or laws are informed by statistics like this! Knowing about measures of center helps us see through misleading statements.

    Here are some guidelines for when to use which measure of center:

    • If the data doesn’t show much skewness or have outliers, mean is the best summary because it incorporates information from every value.

    • If the data has noticeable outliers or skewness, median gives a better summary of center than the mean.

    • If there are very few possible values, such as AP Scores (1–5), mode(s) could be a useful way to summarize the dataset.

    Synthesize

    • What did you learn?

    • What questions surfaced?

    • How did you know whether the questions on Data Cycle Practice were Arithmetic or Statistical?

    🔗Data Exploration Project (Measures of Center) flexible

    Overview

    Students apply what they have learned about measures of center to their chosen dataset, completing the first four rows of the "Measures of Center and Spread" table in their Data Exploration Project Slide Template. They will also interpret those measures of center, and record any interesting questions that emerge.

    Visit Project: Dataset Exploration to learn more about the sequence and scope. Teachers with time and interest can build on the exploration by inviting students to take a deep dive into the questions they develop with our Project: Research Capstone.

    Launch

    Let’s review what we have learned about computing and interpreting three measures of center - mean, median, and modes.

    • Describe how to compute mean, median, and modes.

    • When does mean provide the best summary?

      • It includes information from every single point, so it is useful when the data doesn’t show much skewness or have outliers.

    • When does median provide the best summary?

      • Statisticians fall back to the median when working with highly skewed datasets.

    • When are mode(s) a useful way to summarize a dataset?

      • Mode(s) are most useful when a dataset has very few values.

    Investigate

    Let’s connect what we know about measures of center to your chosen dataset.

    Students have the opportunity to choose a dataset that interests them from our List of Datasets in the Choosing Your Dataset lesson. If you’d prefer to focus your class on a single dataset, we recommend the Global Food Supply & Production Starter File.

    Complete two Data Cycles that use measures of center to help you analyze and understand your chosen dataset.

    Invite students to discuss their results and consider how to interpret them.

    It’s time to add to your Data Exploration Project Slide Template.

    • Locate the "Measures of Center and Spread" section of your Exploration Project and, in the slide following the example, replace Column A with the title of the column you just investigated.

    • Then type in the mean, median and modes that you just identified. Leave the other rows blank. We will come back to them another day.

    • On the next slide, repeat with Column B using the second column you’re interested in.

    • Add your interpretations to the two "Measures of Center and Spread" slides.

    • Record any questions that emerged in the "My Questions" section at the end of the slide deck.

    Synthesize

    Have students share their findings.

    • Did you discover anything surprising or interesting about your dataset?

    • Which measures of center do you think were the most useful for the quantitative columns you chose?

    • What questions did the measures of center inspire you to ask about your dataset?

    • When you compared your findings with other students, did you make any interesting discoveries? (For instance: Did everyone find mode(s)? Did anyone have a measure of center that was dramatically influenced by an outlier?)

    🔗Additional Exercises

    These materials were developed partly through support of the National Science Foundation, (awards 1042210, 1535276, 1648684, 1738598, 2031479, and 1501927). CCbadge Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.