instagram
Lessons

    Aligns to:

    (Also available in Pyret)

    Students build upon their understanding of Booleans and simple inequalities to compose compound inequalities using the concepts of union and intersection.

    Lesson Goals

    Students will be able to:

    • Understand how the conjunctions and and or differ

    • Describe how functions can work together

    • Describe the solution set of a compound inequality

    Student-Facing Lesson Goals

    • Let’s use two or more inequalities together.

    • Let’s learn the difference between how and and or are used in programming.

    • Let’s find solutions and non-solutions for compound inequalities.

    Materials

    Supplemental Materials

    Preparation

    • There is an optional interactive Desmos activity in the lesson. If you would like to use it, decide how you will share it with students and, if you are using our Google Slides, add the appropriate link to the slide deck. If you’re a first-time Desmos user, fear not!__Here's what you need to do._

    🔗Introducing Compound Inequalities

    Overview

    Students consider the need to compose inequalities, and think about how to write them.

    Launch

    We use inequalities for lots of things:

    • Is it hot out? (𝑡𝑒𝑚𝑝𝑒𝑟𝑎𝑡𝑢𝑟𝑒 > 80°)

    • Did I get paid enough for painting that fence? (𝑝𝑎𝑖𝑑 ≥ $100)

    • Are the cookies finished baking? (𝑡𝑖𝑚𝑒𝑟 = 0)

    What other examples can you come up with?

    Many times we need to combine inequalities to answer our questions:

    • We use and when we need both inequalities to be true.

    • We use or when we need at least one of the inequalities to be true.

    For Example:

    • Could it snow?

      • 𝑡𝑒𝑚𝑝𝑒𝑟𝑎𝑡𝑢𝑟𝑒 ≤ 32°F and 𝑡𝑒𝑚𝑝𝑒𝑟𝑎𝑡𝑢𝑟𝑒 ≥ 10°F

    • Is the baby too big for an infant car seat?

      • 𝒽𝑒𝑖𝑔𝒽𝑡 ≥ 30" or 𝑤𝑒𝑖𝑔𝒽𝑡 ≥ 30 𝑝𝑜𝑢𝑛𝑑𝑠

    • Should I go swimming outside?

      • 𝑡𝑒𝑚𝑝𝑒𝑟𝑎𝑡𝑢𝑟𝑒 > 75°F and 𝑤𝑒𝑎𝑡𝒽𝑒𝑟 <> "𝑙𝑖𝑔𝒽𝑡𝑛𝑖𝑛𝑔"

    Can you think of examples of when we might want to combine inequalities?

    We know that it could snow if 𝑡𝑒𝑚𝑝𝑒𝑟𝑎𝑡𝑢𝑟𝑒 ≤ 32°F and 𝑡𝑒𝑚𝑝𝑒𝑟𝑎𝑡𝑢𝑟𝑒 ≥ 10°F.

    • Would this expression be true if the temperature was 30°F? How do you know?

      • Yes. 30 is both below 32 and higher than 10.

    • Would this expression be true if the temperature was 5°F? How do you know?

      • No. While 5 is less than 30, it’s not greater than 10. 5°F is too cold to snow.

    We know that the baby is too big for an infant seat if 𝒽𝑒𝑖𝑔𝒽𝑡 ≥ 30" or 𝑤𝑒𝑖𝑔𝒽𝑡 ≥ 30 𝑝𝑜𝑢𝑛𝑑𝑠

    For each baby below, decide whether the baby needs a bigger car seat and explain how you know.

    • Baby 1 - Height: 32", Weight: 35 pounds

      • Yes. They are too tall and too heavy an infant car seat.

    • Baby 2 - Height: 33", Weight: 22 pounds

      • Yes. They are too tall for an infant car seat.

    • Baby 3 - Height: 20", Weight: 15 pounds

      • No. They are short enough and light enough for an infant car seat.

    • Baby 4 - Height: 29", Weight: 35 pounds

      • Yes. They are too heavy for an infant car seat.

    Stand if it’s True for you!

    Practicing whether compound inequalities will be true or false makes for a great sit-down, stand-up activity, where students take turns saying compound Boolean statements and everyone stands if that statement is true for them.

    • "I’m wearing a red shirt AND I’m a math teacher, true or false?"

    • "I’m an NBA basketball star OR I’m having pizza for lunch, true or false?"

    Expressions using and only produce true if both of their sub-expressions are true.
    Expressions using or produce true if either of their sub-expressions are true.

    Investigate

    Both mathematics and programming have ways of combining - or composing - inequalities.

    Complete Converting Circles of Evaluation to Code and Compound Inequalities - Practice.

    Synthesize

    Be careful to check for understanding here.

    • What is the difference between combining inequalities using and and or?

      • Expressions using and only produce true if both of their sub-expressions are true.

      • Expressions using or produce true if either of their sub-expressions are true.

    Strategies for English Language Learners

    When describing compound inequalities, be careful not to use "English shortcuts". For example, we might say "I am holding a marker and an eraser" instead of "I am holding a marker and I am holding an eraser." These sentences mean the same thing, but the first one obscures the fact that "and" joins two complete phrases. For ELL/ESL students, this is unnecessarily adds to cognitive load!

    🔗Solutions and Non-Solutions of Compound Inequalities

    Launch

    Complete Compound Inequality Warmup.

    Investigate

    When students click "Run", four graphs will appear. The top two are the simple inequalities they’ve just discussed. Encourage students to verify that their solutions and non-solutions are correct.

    • The bottom two graphs are produced by the special functions and-intersection and or-union.

    • Read the comments in the Definitions area with your partner to learn how these functions are supposed to work.

    • Then complete Exploring Compound Inequalities.

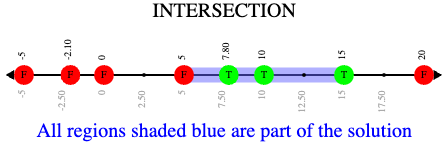    A compound inequality displayed on a number line, showing that the inequalities intersect between 5 and 15. The dot on 5 is red. The dot on 15 is green.x > 5 and x ≤ 15

    • What does it mean that initial circle on 5 is red and the circle on 15 is green?

      • The circle on 5 is red because 5 is not part of the solution - it is not bigger than itself.

      • The circle on 15 is green because 15 is part of the solution - it is less than or equal to 15.

    A compound inequality displayed on a number line, showing no intersection and therefore no solutionsx < 5 and x ≥ 15

    • Why isn’t there a solution to 𝑥 < 5 𝑎𝑛𝑑 𝑥 ≥ 15

      • There aren’t any numbers that are both smaller than 5 and greater than or equal to 15, so there is no solution!

    or-union takes in two functions and a list of numbers and produces a graph with the points and the shaded union of values that make either or both of the inequalities true.

    In order to make an or statement true, a value only has to make one of the inequalities true.

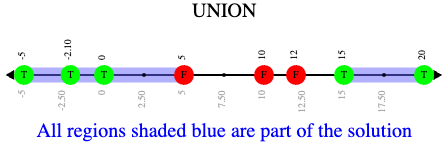    A compound inequality displayed on a number line, shaded when numbers are below 5 or greater than 15. The dot on 5 is red and the dot on 15 is green.x < 5 or x ≥ 15

    Sometimes unions are represented by two separate arrows pointing in opposite directions with a gap between their starting points.

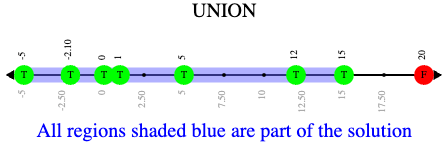    A compound inequality displayed on a number line, shaded when numbers are below 3. The dots on 3, 3.5, 4 and 5 are red and the dots on -5, -2.1, 0 and 1 are green.x < 5 or x ≤ 15

    Sometimes unions overlap and appear as a single arrow pointing in one direction.

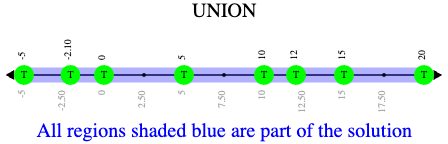    A compound inequality displayed on a number line, showing an infinite unionx > 5 or x ≤ 15

    Sometimes unions overlap and cover the entire number line!

    A compound inequality displayed on a number line, showing an infinite unionx > 5 or x ≤ 15

    • Why is the whole graph of 𝑥 > 5 𝑜𝑟 𝑥 ≤ 15 shaded blue?

      • Because every number in the universe is either greater than 5 or less than or equal to 15, so there aren’t any non-solutions!

    Once students are familiar with the starter file, they are ready to use it as they practice identifying solutions and non-solutions for compound inequalities.

    Instead of defining two functions as simple inequalities, we can produce an inequality graph by defining one function to be a compound inequality!

    • What do you Notice about how the code works?

      • Answers will vary. Facilitate a conversation to draw out all of the things students will need to understand in order to write definitions for the remaining examples!

      • We see that the left end of the shaded region is at 0 and the dot on zero is red so it’s not part of the solution set.
        This tells us that the first inequality is 𝑥 > 0.

      • We see that the right end of the shaded region is at 8.1 and the dot on zero is green so it is part of the solution set.
        This tells us that the second inequality is 𝑥 ≤ 8.1.

      • Since the shaded area is where these two inequalities overlap, we know that it’s a union, which means they are linked with and.

      • Each of the simple inequality expressions is enclosed in a set of parentheses.

      • The definition starts with define.

    • What do you Wonder?

      • Answers will vary, but make space for questions.

    • With your partner, define compound inequality functions for the remaining graphs on the page.

    Synthesize

    • How did the graphs of intersections and unions differ?

      • Intersections were where the two inequalities overlapped. Sometimes they are finite sections of the number line (represented by a segment with dots at both ends) and sometimes they are infinite (represented by an arrow)

      • Unions include everything that was part of either inequality. They can look like a segment, a single arrow, or two arrows.

    🔗Additional Exercises

    Converting Circles of Evaluation with Booleans to Code 2

    These materials were developed partly through support of the National Science Foundation, (awards 1042210, 1535276, 1648684, 1738598, 2031479, and 1501927). CCbadge Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.