instagram

(Also available in WeScheme)

Students explore the concept of slope and y-intercept in linear relationships, using function definitions as a third representation (alongside tables and graphs).

Lesson Goals

Students will be able to…​

  • identify linear and nonlinear graphs and tables

  • identify the slope and y-intercept for a linear relationship shown as a table or graph

  • match different representations of the same linear relationship

Student-facing Lesson Goals

  • Let’s learn to tell the difference between linear and nonlinear relationships in tables and graphs.

  • Let’s connect graphs to tables that describe the same linear relationships.

  • Let’s compute the slope and y-intercept from a table or graph of a linear relationship.

Materials

Supplemental Materials

Preparation

  • There is an optional interactive Desmos activity in the lesson. If you would like to use it, decide how you will share it with students and, if you are using our Google Slides, add the appropriate link to the slide deck. If you’re a first-time Desmos user, fear not! Here’s what you need to do.

Key Points for the Facilitator

  • Lines are made of points (try to avoid referring to "lines" as much as "collections of points")

  • Linear functions can be represented as straight lines on a graph or as sequences that change at a constant rate in a table.

🔗Linear, Nonlinear, or Bust! 25 minutes

Overview

Students explore the concept of linearity, as represented in tables and graphs, and then deepen their understanding of linearity, by seeing counterexamples (nonlinear relationships), as well as tables and graphs for which there is no relationship.

Launch

Complete Notice and Wonder (Linearity)

Part 1:

x y

0

0

1

2

2

4

3

6

4

8

graph of a line passing through the points (0,0) (1,2) (2,4) (3,6) (4,8)

  • In Part 1, what did you Notice?

    • Answers will vary.

    • Each (x, y) pair on the table corresponds to a point on the graph.

    • Both the x and y values in the table are increasing by consistent intervals.

    • The points on the graph are connected by a straight line.

  • What did you Wonder?

Part 2:

x y

1

2

2

3

3

4

4

5

5

6
independent dependent

1

20

2

17

3

14

4

11

5

8

  • What strategies did you to answer the questions in Part 2?

  • What would the next pair of x-y values be for each of the tables?

  • What would the y-values be when x is 0?

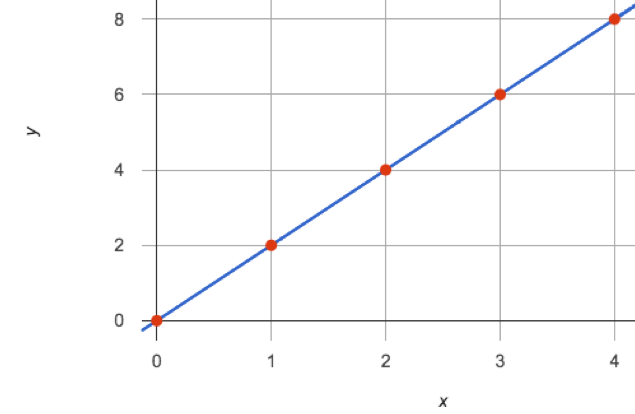
When we notice that x-values change at a constant rate and the y-values also change at a constant rate, we know that there is a linear relationship - plotted on a graph, all of the points will fall on a straight line.

  • Tables only show us some of the points on a line, representing a sample of some larger trend.

  • A line is made up of an infinite number of points. The graph is a way of seeing the trend itself.

  • We can follow the pattern to identify additional points with the same relationship.

Even when we describe a linear relationship with a table that only includes integers, the line connecting those points would include points with fractional and decimal values!

Linear Relationships are sequences where the x and y-values change in proportion with one another, forming a straight line that rises or falls at a constant rate, and includes infinite other points satisfying the same rule.

The points in a table are discrete.

  • Ordering the rows in a table can make it easier for us to find the function.

  • But the rows can be shuffled into a different order.

On a graph, the x-axis must always be ordered.

  • We can stretch the scale of the axes to making the lines look different.

  • But the points will always be in the same order.

Axes on a graph need an order. Rows in a table don’t!

Investigate

Complete the Notice and Wonder on Are All Graphs Linear?

On this page, students will refer to the six graphs below to consider the question:
If all linear relationships can be shown as points on a graph, does that mean all graphs are linear?

1)

horizontal line crossing the y-axis at 48

2)

upside-down v-shaped graph with its vertex at the origin

3)

two curves: one rounds down from (-7.5, 2.75) to the origin and the other curves up from the origin to (7.5, 2.75)

4)

a diagonal line, sloping downward from left to right

5)

a diagonal line, sloping updward from left to right

6)

a u-shaped graph, opening upward, with its vertex at the origin

  • What do you Notice?

  • What do you Wonder?

  • If all linear relationships can be shown as points on a graph, does that mean all graphs are linear?

    • All of the graphs follow patterns, meaning we know where the next point should go. But, only three of the graphs above represent linear relationships.

    • As we can see, the linear graphs can go in lots of directions.

On a graph, linear relationships always appear as straight lines.

Complete the Notice and Wonder on Are All Tables Linear?.

On this page, students will refer to the six tables below to consider the question:
If all linear relationships can be shown as tables, does that mean all tables are linear?

Note: In preparation for future conversations, students are asked to identify the y-value when x=0.
(This is not yet being described as the y-intercept!)

A

x

-2

-1

0

1

2

 

y

-2

-3

-4

-5

-6

 

B

x

2

4

6

8

10

 

y

-12

-16

-20

-24

-28

 

C

x

1

2

3

4

5

 

y

1

4

9

16

25

 

D

x

5

6

7

8

9

 

y

3

3

3

3

3

 

E

x

1

2

3

4

5

 

y

84

94

104

114

124

 

F

x

-10

-9

-8

-7

-6

 

y

- 1/10

- 1/9

- 1/8

- 1/7

- 1/6

 

  • What do you Notice?

  • What do you Wonder?

  • If all linear relationships can be shown as tables, does that mean all tables are linear? Did you find any tables that could not represent linear relationships?

    • Tables C and F are not linear. The other four tables could be linear.

  • How did you make your predictions about what the next pair of x-y values would be?

    • Answers will vary, but should involve looking for patterns.

  • How did you identify the y-values when x=0 (for the tables that appeared to be linear)?

    • Answers will vary, but will most likely involve extending the tables.

As we saw in the tables, as the x-value increases in linear relationships, the y-values can change in many ways:

  • by zero (no change)

  • by a positive number (constant increase)

  • by a negative number (constant decrease)

In a table representing a linear relationship, a change in the independent variable corresponds to a proportional change in the dependent variable.

  • Take a look at this table and graph.

  • Can you predict the next row of the table or the next point on the graph?

x y

0

13

1

-2

1

16

3

0

4

54

scatter plot with no apparent pattern

Sometimes there is no function that will give us a particular table or graph!

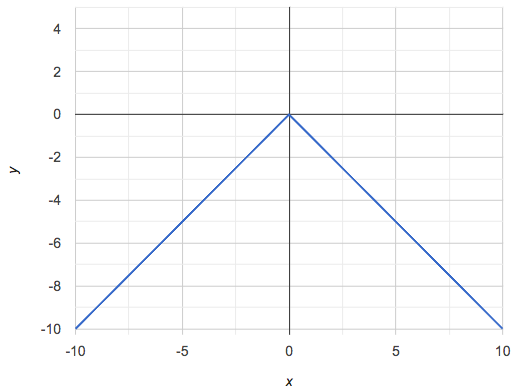
  • How do we know whether a graph represents a function?

    • It has to pass the vertical line test! There should be exactly one y-value for each x-value.

    • Note: We discuss this concept in depth in our lesson on The Vertical Line Test.

Complete Linear, Non-linear, or Bust?.

Data has a "shape", and this shape can emerge when we look for patterns in that data. A linear function is one kind of pattern, and we can see it whether viewing data as a table or a graph.

Synthesize

  • How can we recognize a linear relationship in a table?

  • How can we recognize a linear relationship on a graph?

🔗Slope and y-Intercept from Tables 20 minutes

Overview

Students refine their understanding of linearity, identifying properties like slope and y-intercept in tables.

Launch

Every linear relationship has two properties:

  1. The sequence of y-values always changes at a constant rate - called slope - increasing or decreasing by the same amount for each change in the x-value.

  2. The y-value when x = 0 is called the y-intercept.

x

-1

0

1

2

3

4

y

-1

1

3

5

7

9

  • The slope is how much y increases as x increases by 1. What is the slope?

    • We can see that the y-values increase by 2 each time x increases by 1, giving us a slope of 2.

    • Some students may need an explicit demonstration of subtracting two adjacent y-values in order to recognize that they are changing by 2.

  • Identify the y-intercept by finding the y-value when x = 0.

    • The y-intercept is 1.

  • What strategies did you use to compute the slope and y-intercept?

    • Leave some time for group discussion of strategies!

Before we move on to finding the slope from more complicated tables, let’s get some more practice!
Complete Slope & y-Intercept from Tables (Practice).

Investigate

Life isn’t always so simple!

  • What if the table didn’t include x = 0?

  • What if the x-values didn’t increase by 1?

  • What if the x-values were out of order?

  • What if we only had two random coordinate pairs?

Consider the second table on the page:

x

3

6

9

12

y

4

9

14

19

  • Try extending the table and filling in the missing points to find the slope and y-intercept.

  • What strategies did you use to extend the table?

To find the slope and y-intercept for functions like this one, without having to extend the table we can exploit the fact that all linear functions form straight lines, and a straight line can be defined with only two points!

It is always possible to compute slope and y-intercept, as long as we have two coordinate pairs!

x

3

6

9

12

y

4

9

14

19

Take a few minutes to brainstorm about how we might compute the slope using only two points from the table. Would your strategy work if the points weren’t adjacent to (next to) each other in the table?

Leave some time for group discussion…​

TO FIND THE SLOPE: Find any two pairs of values in the table, and divide the difference in y’s by the difference in x’s.

This lets us see the change in y as a proportion of the change in x, which gives you the slope of the function.

This strategy is often described by the algorithm $$\displaystyle {{\text{ChangeInY}} \over\displaystyle {\text{ChangeInX}}} or {{\text{Rise}} \over\displaystyle {\text{Run}}}$$.

x

3

20

5

9

1

y

5

56

11

23

-1

Taking the first two pairs of (x,y) coordinates in the the last table on the page, gives us:

$$\displaystyle {{56 - 5} \over\displaystyle {20 - 3}} = {51 \over\displaystyle 17} = 3$$

We would get the same answer for this example if we subtracted the (x,y) coordinates in the opposite order…​

$$\displaystyle {{5 - 56} \over\displaystyle {3 - 20}} = {-51 \over\displaystyle -17} = 3$$

But if we mixed subtracted the x-values in a different order than we subtracted the y-values, we’d get the wrong answer!

$$\displaystyle {{56 - 5} \over\displaystyle {3 - 20}} = {51 \over\displaystyle -17} = -3$$

We can work with the two points in any order, but we need to use the same order for our x’s as we use for our y’s.

While we can find the slope from any two points in a table, there is often an easiest pair to work with. For example, points that are adjacent to each other, points that have whole number values, etc.
Encourage students to make conscious choices as they work so that they are working smarter not harder!

  • Pick two other pairs of values from the third table and compute the slope. Did you get the same answer?

  • Are there other strategies we could have used to find the slope?

The focus here is on finding the slope from two points. Finding the y-intercept from two points is significantly more involved - we discuss strategies for that in detail in our Defining Linear Functions lesson.

Let’s practice identifying the slope of a linear function when tables aren’t organized to make the pattern jump out at us by completing Identifying Slope in Tables.

Slope and y-intercept form the essence of linear functions. If we can find them in a sample of data, we can make predictions that go outside that sample. For example: If we know a car is moving at a consistent speed, all we need to know is where it is located at two points in time in order to figure out the speed, and to predict where it will be at any other point during its trip!

Synthesize

  • How many points are needed to define a line?

    • 2

🔗Slope and y-Intercept from Graphs 15 minutes

Overview

Students refine their understanding of linearity, identifying properties like slope and y-intercept from graphs.

Launch

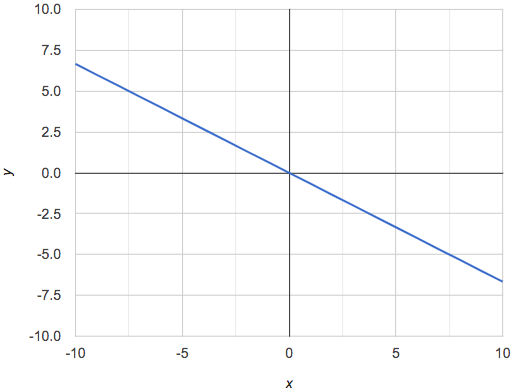
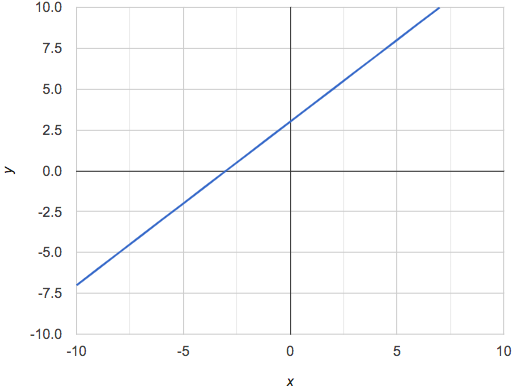
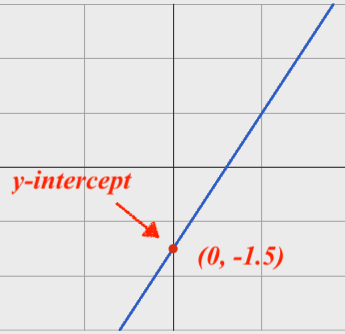
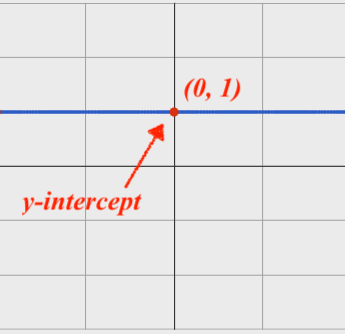
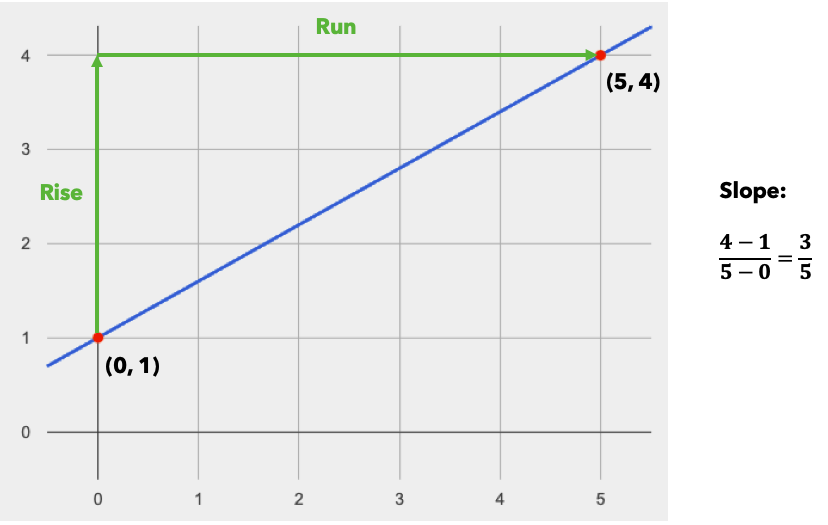
On a graph, the y-intercept is the value where the line "intercepts" the y-axis.

graph: diagonal line crosses the y-axis at (0,-1.5)

graph: horizontal line crosses the y-axis at (0,1)

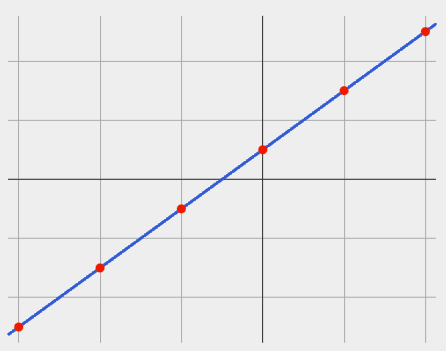
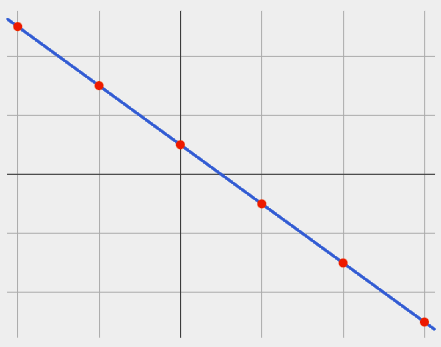
On a graph, the slope refers to both the "steepness" and "direction" of the line.

If it goes up as we go from left to right, the slope is positive.

If it goes down as we go from left to right, the slope is negative.

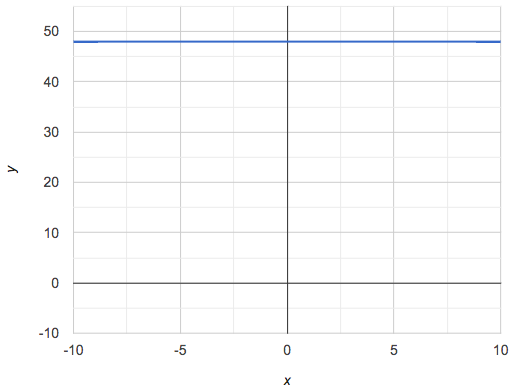
If it stays perfectly horizontal, the slope is zero.

graph: diagonal line sloping upwards from left to right

graph: diagonal line sloping downward from left to right

graph: horizontal line

We can compute the slope from a graph the same way we would with a table, by picking two points we know the exact coordinates of.

graph of a diagonal line passing through (0,1) and (5,4) showing how to calculate the slope is 3/5

Investigate

Let’s get some practice identifying the slope and y-intercept of a linear function in a graph by completing Identifying Slope and y-intercept in Graphs

Pedagogy Note

Some texts refer to "four ways to draw straight lines on a graph": sloping up and to the right, down and to the left, horizontal, or vertical. When thinking only in terms of straight lines on a graph, this is technically correct! However, just because we can draw those lines doesn’t make them functions, and it doesn’t mean they all have a defined slope!

Once students are comfortable computing slope, try having them compute the slope of a vertical line. They will quickly realize that this results in a zero in the denominator, which makes the slope undefined! This can be a good review of divide-by-zero and another lens for thinking about the vertical line test.

Synthesize

We have learned how to find slope and y-intercept from tables and graphs of linear relationships. Looking ahead, we will be learning about yet another representation of Linear Functions that you might find to be even more flexible and powerful.

  • Check in with yourself and what we’ve learned.

    • Which representation do you feel more confident finding the slope from? Why?

    • Which representation do you feel more confident finding the y-intercept from? Why?

  • Linear relationships are everywhere…​

    • "On average, for each extra gallon I pump into my tank, I can drive an additional 31 miles."

    • "For each additional hour Carlo babysits, he earns 15 more dollars."

    • "Each cockroach the lizard eats decreases the number of cockroaches in the house by one."

    • "Every 10 additional people in line for the ride at the amusement park increases the wait time by 3 minutes."

    • What other linear relationships can you think of?

🔗What Stories do they tell us? flexible

Overview

In this section students will have a chance to describe the stories they see in tables and graphs.

Launch

When we are fluent at reading graphs and tables, they tell us a story.

Turn to What Story does the Graph tell? and consider the first example.

  • Based on the example, what are the key components we should include when telling the story of a linear relationship?

    • The starting point, the variables, and the rate of change.

Investigate

Have students work through:

Synthesize

  • Have you thought about graphs and tables as telling stories before?

  • Is it easier for you to read the stories from tables or graphs?

🔗Additional Exercises

Pedagogy Note

To encourage students to look at the points in the table and on the graph, it can be useful to change the scale of the graphs to prevent students from leaning on visual cues like "steepness" to bypass the learning objective.

It can also be useful to list the points in the table out of order, both to focus students' attention on the points and to drive home that rows do not have to be ordered!

These materials were developed partly through support of the National Science Foundation, (awards 1042210, 1535276, 1648684, 1738598, 2031479, and 1501927). CCbadge Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.

Lessons

    Aligns to: