instagram

(Also available in WeScheme)

Students use Circles of Evaluation to visualize the structure of expressions that include exponents.

Lesson Goals

Students will be able to…​

  • Translate between words, mathematical expressions, and Circles of Evaluation.

  • Evaluate expressions involving exponents and one other operation.

  • Evaluate expressions involving exponents and negatives.

Student-facing Lesson Goals

  • Let’s use Circles of Evaluation to visualize the structure of expressions with exponents.

Materials

Key Points For The Facilitator

  • Ensure that students are comfortable evaluating exponents during the Launch. Circles of Evaluation will help students parse expressions that involve exponents.

🔗Expressions with Exponents and One Operation 30 minutes

Overview

Students use Circles of Evaluation, words, and arithmetic to visualize the structure of expressions with exponents and one operation.

Launch

Show students the following expression: 23

  • One way of reading this expression is "two raised to the power of three." Do you know any other ways of translating this expression into words?

    • Two to the third power; two to the third; two cubed

a cube with the dimensions 2 x 2 x 2, composed of 8 individual cubes

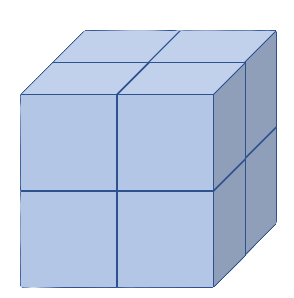
  • What does it mean to cube a number?

    • We multiply it by itself three times. (Literally, we compute the volume of a cube with a side length of that number; see image on right.)

  • What does this expression evaluate to?

    • 23 = 2 × 2 × 2 = 8

Familiarizing ourselves with some exponent terminology makes it easier to talk about exponents.

  • The number on the left is called the base. That number is multiplied by itself when we apply the exponent.

  • The smaller, raised number after the base is called the exponent; it indicates how many times to multiply the base.

  • "Cubing" is the same as "raising to the third power", and "squaring" is the same as raising to the second power.

  • There is no special terminology for any other exponents.

We can represent expressions with exponents as Circles of Evaluation. The function we use to do so is called num-expt; when we use num-expt, the first value in the Circle of Evaluation is the base, and the second value is the exponent.

Look at the two equivalent Circles of Evaluation, below. One is written in exponent notation, and the other is written in expanded notation.

25

2 × 2 × 2 × 2 × 2

(num-expt 2 5)

=

(​* (​* (​* (​* 2 2) 2) 2) 2)

Exponents are valuable because they act as a shorthand.

The Circle of Evaluation with num-expt is a lot shorter and easier to read!

  • Complete Exponent Basics, where you will practice translating verbal exponent expressions into exponent notation, expanded notation, and Circles of Evaluation.

Consider the Circle of Evaluation (below) that Jayla drew to represent the expanded form of 24.

(​* (​* 2 2) (​* 2 2))

  • Jayla’s Circle is different from the solution provided for the first problem on the worksheet. Is her response correct? Why or why not?

    • Yes, we can group the bases in a variety of ways, thanks to the Associative Property of Multiplication!

Ensure that students are comfortable shifting between representations before discussing some common difficulties with interpreting exponents.

52

25

(num-expt 5 2)

(num-expt 2 5)

  • Angela says the Circles of Evaluation above are equivalent because of the Commutative Property. Do you agree with Angela?

    • Angela is incorrect. The first expression evaluates to 25, while the second expression evaluates to 32. We cannot switch the order of the exponent and the base, as we could when adding or multiplying values.

52

5 × 2

(num-expt 5 2)

(​* 5 2)

  • Are these two Circles of Evaluation (above) equivalent? Explain.

    • No; multiplying the base by the exponent is a common student error which produces a different result than multiplying the base by the base.

Let’s explore how Circles of Evaluation can help us when evaluating more complicated expressions with exponents.

Investigate

(​* 9 (num-expt 3 2))

(num-expt (​* 9 3) 2)

  • How would you translate each of these Circles of Evaluation (above) into verbal expressions? Why are their translations different?

    • The Circle of Evaluation on the left is "nine multiplied by three squared," while the Circle of Evaluation on the right is "find the product of nine and three, then square it." Their translations differ because the Circles of Evaluation are organized differently.

  • How would you translate each of these Circles of Evaluation into mathematical expressions?

    • The Circle of Evaluation on the left is 9 × 32 while the Circle of Evaluation on the right is (9 × 3)2.

  • Ada translates the first Circle of Evaluation into this mathematical expression: 9 × 32. Sam translates it like this: 9 × (32). Who is correct?

    • Both students are correct.

While it is acceptable to enclose a base and its exponent in parentheses, expressions with exponents are often written without the parentheses.

In an expression with no grouping symbols, we evaluate the exponent before the other operations.

The first two pages above do not involve any computation; rather, students think about the structure of expressions with exponents and one operation. The third page in the set involves some computation; students who consider structure in addition to computation will complete the activity more efficiently.

Synthesize

  • Is 2 + (62) equivalent to 2 + 62? Why or why not?

    • Yes, these expressions are equivalent. Applying an exponent is a function separate from addition, regardless of whether we put it in parentheses or not.

  • Is 2 + 62 equivalent to (2 + 6)2? Why or why not?

    • No, these expressions are not equivalent. For the first expression, we apply the exponent and then multiply. For the second expression, we multiply and then apply the exponent.

🔗Expressions with Exponents and Variables 25 minutes

Overview

Students use Circles of Evaluation to parse and evaluate exponential expressions with variables.

Launch

Ms. Brenneman asked her class to draw Circles of Evaluation to represent 4m2. Four students produced four different Circles of Evaluation (below).

Keke:

(​* 4 (num-expt 2 m))

Jayla:

(​* 4 (num-expt m 2))

Joe:

(+ 4 (num-expt m 2))

Aaron:

(num-expt (​* 4 m) 2)

  • Which Circle of Evaluation do you think matches the expression 4m2? If you’re not sure, are there any that you can rule out right away?

    • Sample response: Jayla’s Circle of Evaluation is correct. I know that Keke’s response is incorrect because we cannot change the order of the base and the exponent. Joe’s Circle of Evaluation doesn’t work because he added rather than finding a product. Aaron squared 4m, rather than just squaring m.

Keke:

(​* 4 (num-expt 2 m))

Jayla:

(​* 4 (num-expt m 2))

Joe:

(+ 4 (num-expt m 2))

Aaron:

(num-expt (​* 4 m) 2)

Lead a discussion where students explain which Circle of Evaluation they chose and why.

When we evaluate an algebraic expression, we substitute in a given value for the variable and then simplify the expression to a single number. Circles of Evaluation can help us avoid common pitfalls when evaluating algebraic expressions by helping us to see the structure of each expression!

  • Evaluate the Circles of Evaluation made by Keke, Jayla, Joe, and Aaron using m = 5.

    • Depending on your students' level of comfort evaluating algebraic expressions, you may want to complete one or more of the expressions as a class. Try simply replacing the m in each Circle of Evaluation with 5.

  • Do any of the expressions produce the same outcome? Why or why not?

    • Each Circle of Evaluation has a different result because they all have different structures; one Circle of Evaluation even uses addition rather than multiplication. Jayla’s evaluates to 100; Keke’s evaluates to 132; Joe’s evaluates to 29; and Aaron’s evaluates to 400.

We always apply the exponent before applying other operations (unless the parentheses indicate otherwise!).

Investigate

  • Turn to Variable Expressions with Exponents. Draw a Circle of Evaluation to represent each expression that is provided in the left-hand column. The first one is done for you.

  • Once you have completely filled in the Circle of Evaluation column, move to the Evaluate column, where you will evaluate each expression by substituting in the given value.

Common Misconceptions

Students who are new to expressions like 4m2 may misinterpret them. Explain that this notation represents multiplication - not that the 4 and m are contiguous digits.

Synthesize

  • Jayla says that she likes to imagine an "invisible parentheses" enclosing every base and exponent. What is she describing? Do you find this helpful?

  • What was your strategy for evaluating expressions with variables and exponents?

🔗Programming Exploration

Overview

Students apply their knowledge of examples in Pyret to evaluate expressions with exponents.

Launch

  • Complete question 1 on Programming with Exponents. We’ll test these examples in Pyret soon!

  • Which examples did you predict would fail, and why?

Lead a discussion where students share their thinking and strategies for predicting if the examples will pass or fail.

Debrief with students to ensure that they are looking at the messages that appear in Pyret. This activity not only provides practice thinking about evaluating exponents; it also gives students exposure to tests - bits of code used to verify that code is working as we would expect. Examples and tests are widely used in programming! We explore examples in greater depth in Functions: Contracts, Examples & Definitions.

Investigate

A teacher asked her students to make up expressions with exponents that evaluate to 16. She typed their expressions into Pyret as examples to test if they evaluate to 16. Below, place a checkmark next to each of the examples that you predict will pass when you click "Run".

Rather than multiplying the base times itself as many times as the exponent indicates, the students who wrote the failed examples simply multiplied the exponent by the base.

Synthesize

  • What did this programming exploration teach you about Pyret and examples?

  • What did this programming exploration teach you about the evaluating exponents?

These materials were developed partly through support of the National Science Foundation, (awards 1042210, 1535276, 1648684, 1738598, 2031479, and 1501927). CCbadge Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.

Lessons

    Aligns to: