Simple Data Types Contracts Function Composition Defining Values Making Flags Defining Functions Solving Word Problems Structures, Reactors, and Animations Functions That Ask Questions Key Events Refactoring Your Own Drawing Functions Build Your Own Animation Adding Collisions Scoring Adding Levels Making Pong Going Deeper: Nested Structures Feature: Timers
Simple Data Types
Simple Data Types
Students begin to program, explorings how Numbers, Strings, Booleans and operations on those data types work in this programming language.
Lesson Goals |
Students will be able to…
|
Student-facing Lesson Goals |
|
Materials |
|
Preparation |
|
Key Points For The Facilitator |
|
Click here to see the prior unit-based version.
- Boolean
-
a type of data with two values: true and false
- definitions area
-
the left-most text box in the Editor where definitions for values and functions are written
- editor
-
software in which you can write and evaluate code
- error message
-
information from the computer about errors in code
- interactions area
-
the right-most text box in the Editor, where expressions are entered to evaluate
- operator
-
a symbol that manipulates two Numbers and produces a result
- syntax error
-
errors where the computer cannot make sense of the code (e.g. - missing commas, parentheses, unclosed strings)
Numbers & Strings 20 minutes
Overview
Working together using a Driver/Navigator group setup, students experiment with the Editor. They explore Number and String datatypes, and how they behave in this programming language.
Launch
Driver/Navigator
 🖼Show image
When programming in this class, you’ll be working together using the Driver/Navigator model. Each group can only have one "Driver" - their hands are on the keyboard, and their job is to manage the typing, clicking, shortcuts, etc. If you’re not a Driver, you’re a "Navigator" - your job is to tell the Driver where to go, what to type, etc. A good Driver types only what the Navigator tells them to, and a good Navigator makes sure to give clear and precise instructions.
🖼Show image
When programming in this class, you’ll be working together using the Driver/Navigator model. Each group can only have one "Driver" - their hands are on the keyboard, and their job is to manage the typing, clicking, shortcuts, etc. If you’re not a Driver, you’re a "Navigator" - your job is to tell the Driver where to go, what to type, etc. A good Driver types only what the Navigator tells them to, and a good Navigator makes sure to give clear and precise instructions.
The Driver/Navigator Model This model of pair programming is extremely useful for teasing apart the "thinking" step from the "typing" one. Students - especially those who are new to text-based programming or typing itself - can struggle to put their thoughts into the programming environment. This model allows them to focus on communicating their ideas, but letting the Driver focus on the coding. Likewise, the Driver has a chance to focus on syntax and programming. Finally, the requirement that ideas are translated through another person’s hands is an excellent scaffold for getting students talking about their thinking and about code. |
Students should open code.pyret.org (CPO) in their browser, and click "Sign In". This will ask them to log in with a valid Google account (Gmail, Google Classroom, YouTube, etc.), and then show them the "Programs" page. This page is empty - they don’t have any programs yet! Have them click "Open Editor".
Our Editing Environment
 🖼Show image
This screen is called the Editor, and it looks something like the diagram you see here. There are a few buttons at the top, but most of the screen is taken up by two large boxes: the Definitions Area on the left and the Interactions Area on the right.
🖼Show image
This screen is called the Editor, and it looks something like the diagram you see here. There are a few buttons at the top, but most of the screen is taken up by two large boxes: the Definitions Area on the left and the Interactions Area on the right.
The Definitions Area is where programmers define values and functions that they want to keep, while the Interactions Area allows them to experiment with those values and functions. This is like writing function definitions on a blackboard, and having students use those functions to compute answers on scrap paper.
For now, we will only be writing programs in the Interactions Area on the right.
Investigate
Math is a language, just like English, Spanish, or any other language. Languages have nouns (e.g. “ball”, “tomato”, etc.) and verbs, which are actions we can perform on these nouns (e.g. - I can “throw a ball”). Math and programming also have values, like the numbers 1, 2 and 3. And, instead of verbs, they have functions, which are actions we can perform on values (e.g. - “I can square a number”).
Languages also have rules for syntax. In English, for example, words don’t have ! and ? in the middle. In math and programming numbers don’t have & in them.
Languages also have rules for grammar. The cat sat. is a sentence, whereas The sat cat. is nonsense, even though all the words are valid syntax. The order of the words matters!
Keeping the importance of syntax and grammar in mind is helpful when learning to program!.
Have students complete Numbers and Strings (Page 2). Ask them to pay special attention to the error messages!
-
What did you Notice? What do you Wonder?
-
Did you get any error messages? What did you learn from them? Most of the error messages we’ve just seen were drawing our attention to syntax errors: Missing commas, unclosed strings, etc.
Common Misconceptions
In Pyret, writing decimals as .5 (without the leading zero) results in a syntax error. Make sure students understand that Pyret needs decimals to start with a zero!
Synthesize
Our programming language knows about many types of numbers, and they behave pretty much the way they do in math. Discuss what students have learned:
-
Numbers and Strings evaluate to themselves.
-
Our Editor is pretty smart, and can automatically switch between showing a rational number as a fraction or a decimal, just by clicking on it!
-
Anything in quotes is a String, even something like
"42". -
Strings must have quotation marks on both sides.
-
Operators like
+,-,*, and/need spaces around them. -
In pyret, the operators work just like they do in math.
-
Any time there is more than one operator being used, Pyret requires that you use parentheses to define the order of operations.
-
Types matter! We can add two Numbers or two Strings to one another, but we can’t add the Number
4to the String"hello".
Error messages are a way for Pyret to explain what went wrong, and are a really helpful way of finding mistakes. Emphasize how useful they can be, and why students should read those messages out loud before asking for help. Have students see the following errors:
-
6 / 0. In this case, Pyret obeys the same rules as humans, and gives an error. -
(2 + 2. An unclosed quotation mark is a problem, and so is an unmatched parentheses.
Booleans 20 minutes
Overview
This lesson introduces students to Booleans, a unique datatype with only two values: "true" and "false", and why they are useful in both the real world and the programming environment.
Launch
What’s the answer: is 3 greater than 10?
Boolean-producing expressions are yes-or-no questions and will always evaluate to either true (“yes”) or false (“no”). The ability to separate inputs into two categories is unique and quite useful!
For example, some rollercoasters with loops require passengers to be a minimum height to make sure that riders are safely held in place by the one-size-fits all harnesses. The gate keeper doesn’t care exactly how tall you are, they just check whether you are as tall as the mark on the pole. If you are, you can ride, but they don’t let people on the ride who are shorter than the mark because they can’t keep them safe. Similarly, when you log into your email, the computer asks for your password and checks whether it matches what’s on file. If the match is true it takes you to your messages, but, if what you enter doesn’t match, you get an error message instead.
Brainstorm other scenarios where Booleans are useful in and out of the programming environment.
Investigate
In pairs, students complete Booleans (Page 3), making predictions about what a variety of Boolean expressions will return and testing them in the editor.
Synthesize
Debrief student answers as a class.
What sets Booleans apart from other data types?
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Contracts
Contracts
Students learn how to apply Functions in the programming environment and interpret the information contained in Contracts: Name, Domain and Range. Image-producing functions provide an engaging context for this exploration.
Lesson Goals |
Students will be able to:
|
|||||||||||||||
Student-facing Lesson Goals |
|
|||||||||||||||
Materials |
||||||||||||||||
Preparation |
|
|||||||||||||||
Key Points For The Facilitator |
|
|||||||||||||||
Language Table |
|
Click here to see the prior unit-based version.
- argument
-
the inputs to a function; expressions for arguments follow the name of a function
- contract
-
a statement of the name, domain, and range of a function
- contract error
-
errors where the code makes sense, but uses a function with the wrong number or type of arguments
- data types
-
a way of classifying values, such as: Number, String, Image, Boolean, or any user-defined data structure
- domain
-
the type or set of inputs that a function expects
- error message
-
information from the computer about errors in code
- function
-
a mathematical object that consumes inputs and produces an output
- name
-
how we refer to a function or value defined in a language (examples: +, *, star, circle)
- range
-
the type or set of outputs that a function produces
- syntax error
-
errors where the computer cannot make sense of the code (e.g. - missing commas, parentheses, unclosed strings)
- variable
-
a letter or symbol that stands in for a value or expression
Applying Functions 10 minutes
Overview
Students learn how to apply functions in Pyret , reinforcing concepts from standard Algebra, and practice reading error messages to diagnose errors in code.
Launch
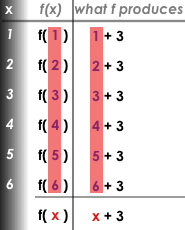
Students know about Numbers, Strings, Booleans and Operators -- all of which behave just like they do in math. But what about functions? Students may remember functions from algebra: fx = x + 4.
-
What is the name of this function? f
-
The expression f2 applies the function f to the number 2. What will it evaluate to? 6
-
What will the expression f3 evaluate to? 7
-
The values to which we apply a function are called its arguments. How many arguments does f expect? 1
Arguments (or "inputs") are the values passed into a function. This is different from variables, which are the placeholders that get replaced with input values! Pyret has lots of built-in functions, which we can use to write more interesting programs.
Have students log into code.pyret.org (CPO) , open the editor, type the words include image on Line 1 of the Definitions area (left side) and press "Run" to load the image library. Then type num-sqrt(16) into the interactions area and hit Enter.
-
What is the name of this function? num-sqrt
-
How many arguments does the function expect? 1
-
What type of argument does the function expect? Number
-
Does the num-sqrt function produce a Number? String? Boolean? Number
-
What did the expression evaluate to? 4
Have students type string-length("rainbow") into the interactions area and hit Enter:
-
What is the name of this function? string-length
-
How many arguments does
string-lengthexpect? 1 -
What type of argument does the function expect? String
-
What does the expression evaluate to? 7
-
Does the
string-lengthfunction produce a Number? String? Boolean? Number
Investigation
Have students complete Applying Functions (Page 4) to investigate the triangle function and a series of error messages. As students finish, have them try changing the expression triangle(50, "solid", "red") to use "outline" for the second argument. Then have them try changing colors and sizes!
Synthesize
Debrief the activity with the class.
-
What are the types of the arguments
trianglewas expecting? A Number and 2 Strings -
How does the output relate to the inputs? The Number determines the size and the Strings determine the style and color.
-
What kind of value was produced by that expression? An Image! New data type!
-
Which error messages did you encounter?
Contracts 15 minutes
Overview
This activity introduces the notion of Contracts, which are a simple notation for keeping track of the set of all possible inputs and outputs for a function. They are also closely related to the concept of a function machine, which is introduced as well. Note: Contracts are based on the same notation found in Algebra!
Launch
When students typed triangle(50, "solid", "red") into the editor, they created an example of a new data type, called an Image.
The triangle function can make lots of different triangles! The size, style and color are all determined by the specific inputs provided in the code, but, if we don’t provide the function with a number and two strings to define those parameters, we will get an error message instead of a triangle.
As you can imagine, there are many other functions for making images, each with a different set of arguments. For each of these functions, we need to keep track of three things:
-
Name — the name of the function, which we type in whenever we want to use it
-
Domain — the type(s) of data we give to the function
-
Range — the type of data the function produces
The Name, Domain and Range are used to write a Contract.
Where else have you heard the word "contract"? How can you connect that meaning to contracts in programming?
An actor signs a contract agreeing to perform in a film in exchange for compensation, a contractor makes an agreement with a homeowner to build or repair something in a set amount of time for compensation, or a parent agrees to pizza for dinner in exchange for the child completing their chores. Similarly, a contract in programming is an agreement between what the function is given and what it produces.
Contracts tell us a lot about how to use a function. In fact, we can figure out how to use functions we’ve never seen before, just by looking at the contract! Most of the time, error messages occur when we’ve accidentally broken a contract.
Contracts don’t tell us specific inputs. They tell us the data type of input a function needs. For example, a Contract wouldn’t say that addition requires "3 and 4". Addition works on more than just those two inputs! Instead, it would tells us that addition requires "two Numbers". When we use a Contract, we plug specific numbers or strings into the expression we are coding.
Contracts are general. Expressions are specific.
Let’s take a look at the Name, Domain, and Range of the functions we’ve seen before:
A Sample Contracts Table
| Name | Domain | Range | ||
|---|---|---|---|---|
|
:: |
|
-> |
|
|
:: |
|
-> |
|
|
:: |
|
-> |
|
|
:: |
|
-> |
|
|
:: |
|
-> |
|
When the input matches what the function consumes, the function produces the output we expect.
Optional: Have students make a Domain and Range Frayer model (Page 5) and use the visual organizer to explain the concepts of Domain and Range in their own words.
Here is an example of another function. string-append("sun", "shine")
Type it into the editor. What is its contract? string-append :: String, String -> String
Investigate
Have students complete pages Practicing Contracts: Domain & Range (Page 6) and Matching Expressions and Contracts (Page 7) to get some practice working with Contracts.
Synthesize
-
What is the difference between a value like
17and a type likeNumber? -
For each expression where a function is given inputs, how many outputs are there? For each collection of inputs that we give a function there is exactly one output.
Exploring Image Functions 20 minutes
Overview
This activity digs deeper into Contracts. Students explore image functions to take ownership of the concept and create an artifact they can refer back to. Making images is highly motivating, and encourages students to get better at both reading error messages and persisting in catching bugs.
Launch
Error Messages The error messages in this environment are designed to be as student-friendly as possible. Encourage students to read these messages aloud to one another, and ask them what they think the error message means. By explicitly drawing their attention to errors, you will be setting them up to be more independent in the next activity! |
Suppose we had never seen star before. How could we figure out how to use it, using the helpful error messages?
-
Type
starinto the Interactions Area and hit "Enter". What did you get back? What does that mean? There is something called "star", and the computer knows it’s a function! -
If it’s a function, we know that it will need an open parentheses and at least one input. Have students try star(50)
-
What error did we get? What hint does it give us about how to use this function?
starhas three elements in its Domain -
What happens if I don’t give it those things? We won’t get the star we want, we’ll probably get an error!
-
If I give
starwhat it needs, what do I get in return? An Image of the star that matches the arguments -
What is the contract for star? star : Number String String -> Image
-
The contract for
squarealso hasNumber String Stringas the Domain andImageas the Range. Does that mean the functions are the same? No! The Domain and Range are the same, but the function name is different… and that’s important because thestarandsquarefunctions do something very different with those inputs!
Investigate
-
At the back of your workbook, you’ll find pages with space to write down a contract and example or other notes for every function you see in this course. The first few have been completed for you. You will be adding to these contract pages and referring back to them for the remainder of this Bootstrap class!
-
Take the next 10 minutes to experiment with the image functions listed in the contracts pages.
-
When you’ve got working expressions, record the contracts and the code!
(If needed, you can print a copy of these contracts pages for your students.)
Strategies for English Language Learners MLR 2 - Collect and Display: As students explore, walk the room and record student language relating to functions, domain, range, contracts, or what they perceive from error messages. This output can be used for a concept map, which can be updated and built upon, bridging student language with disciplinary language while increasing sense-making. |
Synthesize
-
squareandstarhave the same Domain (Number, String, String) and Range (Image). Did you find any other shape functions with the same Domain and Range? Yes!triangleandcircle. -
Does having the same Domain and Range mean that the functions do the same things? No! They make very different images!
-
A lot of the Domains for shape functions are the same, but some are different. Why did some shape functions need more inputs than others?
-
Was it harder to find contracts for some of the functions than others? Why?
-
What error messages did you see? Too few / too many arguments given, missing parentheses, etc.
-
How did you figure out what to do after seeing an error message? Read the error message, think about what the computer is trying to tell us, etc.
-
Which input determined the size of the Rhombus? What did the other number determine?
Contracts Help Us Write Code 10minutes
Overview
Students are given contracts for some more interesting image functions and see how much more efficient it is to write code when starting with a contract.
Launch
You just investigated image functions by guessing and checking what the contract might be and responding to error messages until the images built. If you’d started with contracts, it would have been a lot easier!
Investigate
Have students turn to Using Contracts (Page 8), Using Contracts (continued) and use their editors to experiment.
Once they’ve discovered how to build a version of each image function that satisfies them, have them record the example code in their contracts table. See if you can figure out what aspect of the image each of the inputs specifies. It may help you to jot down some notes about your discoveries. We will be sharing our findings later.
-
What kind of triangle did
trianglebuild? Thetrianglefunction draws equilateral triangles -
Only one of the inputs was a number. What did that number tell the computer? the size of the triangle
-
What other numbers did the computer need to already know in order to build the
trianglefunction? all equilateral triangles have three 60 degree angles and 3 equal sides -
If we wanted to build an isosceles triangle or a right triangle, what additional information would the computer need to be given?
Have students turn to Triangle Contracts (Page 9) and use the contracts that are provided to write example expressions. If you are ready to dig into triangle-sas, you can also have students work through Triangle Contracts (SAS & ASA).
Sometimes it’s helpful to have a contract that tells us more information about the arguments, like what the 3 numbers in a contract stand for. This will not be a focal point of our work, but to give students a taste of it, have them turn to Radial Star (Page 10) and use the contract to help them match the images to the corresponding expressions. For more practice with detailed contracts you can have them turn to Star Polygon to work with the detailed contract for a star-polygon. Both of these functions can generate a wide range of interesting shapes!
Synthesize
Make sure that all students have completed the shape functions in their contracts pages with both contracts and example code so they have something to refer back to.
-
How was it different to code expressions for the shape functions when you started with a contract?
-
For some of you, the word
ellipsewas new. How would you describe what an ellipse looks like to someone who’d never seen one before? Why did the contract forellipserequire two numbers? What happened when the two numbers were the same?
How to diagnose and fix errors is a skill we will continue working on developing. Some of the errors are syntax errors: a missing comma, an unclosed string, etc. All the other errors are contract errors. If you see an error and you know the syntax is right, ask yourself these three questions:
-
What is the function that is generating that error?
-
What is the contract for that function?
-
Is the function getting what it needs, according to its Domain?
Common Misconceptions
Students are very likely to randomly experiment, rather than to actually use the Contracts. You should plan to ask lots of direct questions to make sure students are making this connection, such as:
-
How many items are in this function’s Domain?
-
What is the name of the 1st item in this function’s Domain?
-
What is the type of the 1st item in this function’s Domain?
-
What is the type of the Range?
Additional Exercises:
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Function Composition
Function Composition
Students learn to combine image transformation functions as well as to describe the order of operations involved in algebraic function compositions such as f(g(h(x))) using Circles of Evaluation.
Lesson Goals |
Students will be able to:
|
|||||||||||||||
Student-facing Goals |
|
|||||||||||||||
Materials |
||||||||||||||||
Supplemental Resources |
||||||||||||||||
Preparation |
|
|||||||||||||||
Key Points For The Facilitator |
|
|||||||||||||||
Language Table |
|
Click here to see the prior unit-based version.
- contract
-
a statement of the name, domain, and range of a function
- data types
-
a way of classifying values, such as: Number, String, Image, Boolean, or any user-defined data structure
- definitions area
-
the left-most text box in the Editor where definitions for values and functions are written
- image
-
a type of data for pictures
- interactions area
-
the right-most text box in the Editor, where expressions are entered to evaluate
Composing Functions 10 minutes
Students are given a scaffolded activity that forces them to use the output of one function as the input to another - to compose them.
Launch
Divide students into groups of 3-4, and distribute a set of Function Cards to each group. Write down pairs of integers on the board, representing the "starting numbers" and "ending numbers". These integers should range from -50 to +50, but you can change the difficulty of the activity by making that span wider (more difficult) or more narrow (less difficulty). You can find a random integer generator here.
-
Each group has a set of functions, each of which takes an input and produces an output. I can start with the number
4, for example, and give it to the functionadd6. What will the output be? 10 -
I can also compose functions, meaning that the output of one is immediately passed into another. For example, I could compose
add6anddouble, so the10gets passed into the next function, and doubled to produce20. What would happen if I composedadd6withdoubleand withhalf? 10 -
For each of the starting numbers on the board, your job is to figure out which functions to compose in order to get to the end.
-
You will need to use some functions more than once, and that’s ok!
Investigate
Give students time to experiment with this. You can make the activity more challenging by asking them to find the shortest path from start to end, using the smallest number of compositions.
Synthesize
If two groups come up with different compositions that achieve the same end result, have them share their ideas!
Diagramming Function Composition
Overview
The Circles of Evaluation are extended to provide a visual-spatial metaphor for function composition, in addition to Order of Operations.
Launch
Three of the function cards we just used were for the functions f, g and h:
-
fmultiplied its input by 3 -
gadded six to its input -
hsubtracted one from its input
We can compose those function in any order. If we composed them as f(g(h(x))) and evaluated them for x = 4 what would happen?
We can diagram the function composition using Circles of Evaluation (see first column, below). In the second column, we’ve replaced the function names in each Circle of Evaluation with what each function does:
| Function Composition | Order of Operations | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
(f (g (h x))) |
(* 3 (+ (- x 1) 6)) |
The circles show us that in order to evaluate f(g(h4)))
-
First we would have to evaluate h4, subtracting
1from4to get3 -
Then we would evaluate g3, adding
6to3to get9 -
Then we would evaluate f27, tripling
9to get27
Investigate
Have students turn to Diagramming Function Composition (Page 12) to practice writing, translating and evaluating Circles of Evaluation of composed functions.
Synthesize
Do f(g(hx)) and g(h(fx)) evaluate to the same thing? No!
Why not? order matters!
Composing Functions in Code 20 minutes
Overview
The Circles of Evaluation are extended to functions that do more than compute values.
Launch
The contracts page in your workbook is just like the Function Cards from this activity. Your job as a programmer is to figure out how to compose those functions to get where you want to go, in the most clever or elegant way possible.
Investigate
Have students log into code.pyret.org (CPO) open a new program and save it as Function Composition.
Have students open to Function Composition — Green Star (Page 13), in which they will be drawing circles of evaluation to help them write expressions to compose a series of images.
-
Make sure students are using the Definitions area (left side) for code they want to keep and are using the Interactions area (right side) to test code or try out new ideas.
-
When students are finished, check their work, and ask them to change the color of all of the stars to “gold” or another color of your choosing.
Then have students open to Function Composition — Your Name (Page 14) in which they will create a text image of their name and experiment with other functions.
Strategies for Facilitation While students are exploring, be available for support but encourage student discussion to solve problems. Many student questions can be addressed with these responses: Did you try drawing the Circle of Evaluation first? Did you check the contract? Have you pressed the Run button to save your Definitions changes? Encourage students to practice writing comments in the code to describe what is being produced, using |
If you have time, you can also have students work with Function Composition — scale-xy (Page 15) and/or Function Composition Matching Activity (Desmos)
Synthesize
-
What do all of these functions have in common? They all produce images, they all change some element of the original image
-
Does using one of these functions change the original image? No, it creates a whole new image
-
What does the number in scale represent? The scale factor by which the image should grow or shrink
-
What does the number in rotate represent? The rotation angle, measured counterclockwise
-
The Domain and Range for flip-horizontal is Image -> Image. Why can I use the output of the text function as an input for flip-horizontal? Because the text function produces an Image, which is then used as the input for flip-horizontal.
Strategies for English Language Learners MLR 1 - Stronger and Clearer Each Time: As an alternative, display the discussion questions during the last 5 minutes of the Explore and ask students to discuss the questions with their partner, asking each other for explanation and details and coming up with the clearest, most precise answer they can. Student pairs can then share with another pair and compare their responses before moving into a full class discussion. |
Fun with Images! Now that students have learned how to use all of these image-composing functions, you may want to give them a chance to create a design of their own, tasking them with using at least 4 functions to create an image of their choosing. Our Flags lesson also dives deeper into image composition. |
Composing Multiple Ways Optional
Overview
Students identify multiple expressions that will create the same image, and think about the merits of one expression over another.
Launch
As is often true with solving math problems, there is more than one way to get the same composed image.
Suppose I wrote the code: scale(3, star(50, "solid", "red")).
What’s another line of code I could write that would produce the exact same image? star(150, "solid", "red")
Investigate
Students complete More than one way to Compose an Image! (Page 16).
Synthesize
There is a special function in code.pyret.org (CPO) that let’s us test whether or not two images are equal.
is-image=:: Image, Image -> Boolean
Use it to test whether all of the expressions you wrote successfully build the same images.
-
Could we have written more expressions to create the same images?
-
Are all of the ways to write the code equally efficient?
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Defining Values
Defining Values
Students learn to improve readability, performance and maintanability of code by defining values that repeat in code, just as we would define variables in math.
Lesson Goals |
Students will be able to:
|
|||||||||||||||
Student-facing Goals |
|
|||||||||||||||
Materials |
||||||||||||||||
Preparation |
|
|||||||||||||||
Key Points For The Facilitator |
|
|||||||||||||||
Language Table |
|
Click here to see the prior unit-based version.
- contract
-
a statement of the name, domain, and range of a function
- data types
-
a way of classifying values, such as: Number, String, Image, Boolean, or any user-defined data structure
- definitions area
-
the left-most text box in the Editor where definitions for values and functions are written
- value
-
a specific piece of data, like 5 or "hello"
- variable
-
a letter or symbol that stands in for a value or expression
What’s in Common? 30 minutes
Overview
This activity introduces the problem with duplicate code, leveraging Mathematical Practice 7 - Identify and Make Use of Structure. Students identify a common structure in a series of expressions, and discover how to bind that expression to a name that can be re-used.
Note that in Pyret definitions work the way variable substitution does in math, as opposed to variable assignment you may have seen in other programming languages.
Launch
Take a look at the expressions below:
star(50, "solid", "green")
scale(3, star(50, "solid", "green"))
scale(0.5, star(50, "solid", "green"))
rotate(45, star(50, "solid", "green"))
rotate(45, scale(3, star(50, "solid", "green")))-
What code do they all have in common?
star(50, "solid", "green") -
What would happen if you were asked to change the color of all the stars to gold? We’d have to change it everywhere it appeared.
Duplicate code is almost always bad!
There are lots of potential problems with duplicate code:
-
Readability: The more code there is, the harder it can be to read.
-
Performance: Why re-evaluate the same code a dozen times, when we can evaluate it once and use the result as many times as we need?
-
Maintainability: Suppose we needed to change the size of the stars in the examples above. We would have to make sure every line is changed, which leaves a lot of room for error.
Since we’re using that star over and over again, wouldn’t it be nice if we could define a "nickname" for that code, and then use the nickname over and over in place of the expression? And then, if we wanted to change something about all of the stars, we would only have to make the change once, in the definition.
You already know how to do this in math:
x = 4 defines the nickname x to be the value 4.
Pyret is no different!
We type x = 4 to define x to be the value 4.
Once we’ve defined x to be the value 4 and clicked "run", anytime we use x, the computer will remember that it is defined as 4. We can use that definition to get an answer. For example, x + 2 will evaluate to 6.
Of course, the whole point of defining a value is so that it sticks around and can be used later! That’s why programmers put their definitions on the left-hand side, known as the Definitions Area.
Investigate
-
Open the Defining Values Starter File (Pyret) and complete the notice and wonder exercise on Defining Values - Explore (Page 18) with your partner.
-
Complete the remaining questions and add some defintions of your own in the definitions area. Be sure to click Run again before you try testing them out.
Synthesize
-
What data types can we define values for? All of them - Number, String, Image
-
What values did you decide to define? When might they be useful?
Support for English Language Learners MLR 8 - Discussion Supports: As students discuss, rephrase responses as questions and encourage precision in the words being used to reinforce the meanings behind some of the programming-specific language, such as "define" and "value". |
Using Defined Values
Overview
Now that we know how to define values, we’ve got two more things to consider:
-
When it would be useful to define them
-
How to use them once we have
Launch
Have students open to Defining Values - Chinese Flag (Page 19). It will direct them to open the Chinese flag Starter File (Pyret) once they complete the first half of the questions on the page.
Investigate
-
Have students open the editor and type radial-star(30, 20, 50, "solid", "yellow") into the interactions area and click run.
-
Have students work in the Definitions area to define a value
sunto be the image radial-star(30, 20, 50, "solid", "yellow").
-
Turn to Why Define Values? (Page 20). The first row of the table has been completed for you. Could I get a volunteer to explain what they see happening in that first row?
-
Have students complete the page and test their code in the editor.
Synthesize
-
Why is defining values useful? Lets the programmer reuse code, saves time, lets the programmer make changes easily, allows us to more easily use elements inside other functions
Additional Exercises:
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Making Flags
Making Flags
Students recreate images of flags of varying complexity by transforming and composing image functions and applying their knowledge of ratios and coordinates to scale and position the shapes precisely.
Lesson Goals |
Students will be able to:
|
|||||||||||||||
Student-facing Goals |
|
|||||||||||||||
Materials |
||||||||||||||||
Supplemental Resources |
|
|||||||||||||||
Preparation |
|
|||||||||||||||
Key Points For The Facilitator |
|
|||||||||||||||
Language Table |
|
- contract
-
a statement of the name, domain, and range of a function
Putting Images Together 25 minutes
Overview
Students learn about the put-image function.
Launch
As you’ve already seen, overlay sticks two images together, so that the center of the first image is placed exactly on top of the center of the second image. But what if we want to put the dot somewhere besides the center?
The put-image function works like overlay, but instead of placing the centers of each image on top of one another, it translates the center of the top image by some distance in the x- and y-direction.
Think of the background image as a sheet of graph paper with the origin (0,0) in the bottom left corner.
The numbers in put-image specify a point on that graph paper, with the center of the top image being placed there.
-
Distribute Estimating Coordinates (Page 23) or project the flag images from the peardeck.
-
The code beneath each image is missing the x and y coordinates to place the dot.
-
Estimate the x- and y-coordinate of the dot’s location for each image and complete the code!
Investigate
Have students open the Flags Starter File , and click Run.
There are some special lines in this file called comments. The programmer who wrote this code included a series of messages - called comments - that will never be read by the computer.
Professional programmers use comments all the time.
Professional programmers work with teams who need to be able to follow each other’s thinking in order to collaborate efficiently. Comments are a way for programmers to leave notes for one another, and even for a single programmer to keep track of their thinking when they come back to their code another day.
-
In Pyret, we use the number sign (
#) to tell the computer to ignore what we’re typing. What color does the code turn when it has a number sign in front of it? Red! -
Type
japan-flaginto the Interactions Area. What do you get back? -
Type
japaninto the Interactions Area and compare the image tojapan-flag. -
japanis composed usingdotandbackground. Type each of those variables into the Interactions Area. What do you get back? -
Take a look at the
japancode and fix it so that it matches thejapan-flagimage. -
What is the Contract for
put-image? (Write it in your Contracts page!)
Have students open the Flags of Netherlands, Ireland, Mauritius Starter File , and click Run.
-
Look at the code for the flag of the Netherlands.
-
How big is the flag?
-
What was the programmer thinking when she coded the height of the red stripe as 200 / 3?
-
The center of the blue stripe is placed at (150, 200 / 6). How did the programmer know to use 150 as the x-coordinate?
-
What was the programmer thinking when she coded the y-coordinate as 200 / 6?
-
Explain the thinking behind coding the redstripe’s y-coordinate as 5 * (200 / 6).
Once you’ve discussed the code for the flag of the Netherlands with your class, have them keep working with this starter file to write code for the flags of Ireland and Mauritius. Some students will make it through the challenges. Some students may only complete one flag. All of them will be synthesizing how to apply put-image and locate images on the coordinate grid.
Synthesize
Could we completely replace overlay with put-image? Why or why not?
Going Deeper If you have time, we have lots of additional starter files to push student thinking linked in the additional exercises at the end of this lesson and now would be the time to dive into them! |
Making Flags 25 minutes
Overview
Students focus on decomposing complex images into simple ones, and using put-image to combine them.
Launch
Let’s dig into the process for how the flags we’ve seen so far were made:
1) Decompose the Image
We observe that the Japanese flag is made up of two simpler images: a black, outline rectangle and a red dot.
2) Define those parts
We define dot and background. Once we’ve defined those images, we test them out in the Interactions Area to make sure they look right!
3) Find the Coordinates
For each image, calculate what the x- and y-coordinates of the center should be. TIP: this is a lot easier if you have a sheet of graph paper handy!
4) Build the Image & Check that it Matches the Target Image
We stack the parts on top of the bottom image using the coordinates we found. TIP: don’t cram all the code into one line! If you break it up into new lines (for example, hitting "Return" before the x-coordinate and after the y-coordinate), you’ll notice that the code forms a "staircase" pattern. Be sure to compare the image you get with the target image!
If you have time, these matching activities will support student thinking.
Investigate
Paper Flag Models to Code In this next exercise, students will be decomposing the image of a flag. For a more tactile experience, you could have students construct images of the flags they choose using construction paper. This should happen between the step where they describe the shapes needed to compose the flags image and write the code to build the image. The act of physically building the flag from layers of paper makes the layering of the coded images visible and helps students to remember that white space is not just "blank". |
-
Turn to Decomposing Flags (Page 24), and choose ONE flag to focus on. On the blank lines below, describe the parts that make up that flag.
-
Once you’re done, return to the Flags Starter File and define those parts.
-
Then, compose those parts using
put-image, and make your flag!
Around the World in your Classroom The opportunity to focus on a flag of their choosing is a big motivator for students. Coding flags also presents a rare opportunity for students to share a piece of their identity in math class. If you have more time to devote, we highly encourage you to give students the opportunity to create the image of a flag they connect with in some way. Students might choose the flags of countries related to their heritage, a place they’ve visited, a country they’re interested in, or a group they identify with or support. Encourage students to choose an appropriately challenging flag. The teacher may introduce parameters if necessary, such as “Flags need at least 5 different shapes”. This is intended to be a summative project, so encourage students to demonstrate what they’ve learned. Once students have coded their flags, host a tour of the flags of the world in your classroom! Be mindful of the fact that not every student will know their family’s geographical history, and that immigration can be a sensitive topic for some students. For this reason, it is important that students have the option to choose a flag based on interest instead of just family history. Be prepared that students might choose flags representing groups other than countries. Indigenous students might choose a flag that represents their indigenous nation or the American Indian Movement. Students might also choose to focus on the pride flag (representing solidarity amongst members of the LGBTQ community) or an ethnic flag (representing solidarity amongst members of different ethnic groups, such as the Hispanic flag). There are also some flags that represent political or activist groups. It is important for the teacher to be open to different beliefs and ideologies, but it is also up to the teacher’s discretion as to whether or not a flag is appropriate for use in this project. Flags associated with hate groups, or any institution that denies the dignity of other students, are not appropriate. Flags of the World and Flag Wizard may be useful to students looking for ideas. Flags are listed with their width:length ratios in the opposite order of how we define the sides of a flag in code. e.g. 2:3 could be scaled up to a 300 x 200 flag or 8:11 could be scaled up to 330 by 240. |
Ratio and Proportion Have students define the |
Synthesize
Which flags were the easiest to make? The hardest?
Why is it useful to define each part of the flag first, before stitching the images together?
Additional Exercises
-
These two starter files provide students with an image of a flag and code that starts out generating a jumbled pile of shapes. Students work to fix the code by resizing, rotating, and correctly locating the components on the background in order to compose an image that looks like the original flag: Flag of Mexico Starter File (Pyret) and Puerto Rican Flag Starter File (Pyret)
-
For a quick dive into why it’s more efficient to define shapes before building the image, open the Alaska Flag Starter Code. (Pyret)
-
For practice scaling imported graphics, open the Flag of Lebanon Starter Code. (Pyret)
-
If you’ve already studied Pythagorean Theorem and are ready to apply it, open the Flag of Trinidad and Tobago Starter Code. (Pyret)
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Defining Functions
Defining Functions
Students discover that they can make their own functions and are introduced to a structured approach to building them called the Design Recipe.
Lesson Goals |
Students will be able to:
|
|||||||||||||||
Student-Facing Lesson Goals |
|
|||||||||||||||
Materials |
||||||||||||||||
Preparation |
|
|||||||||||||||
Key Points for the Facilitator |
|
|||||||||||||||
Language Table |
|
Click here to see the prior unit-based version
- example
-
shows the use of a function on specific inputs and the computation the function should perform on those inputs
- function
-
a mathematical object that consumes inputs and produces an output
- function definition
-
code that names a function, lists its variables, and states the expression to compute when the function is used
- syntax
-
the set of rules that defines a language, whether it be spoken, written, or programmed.
There’s Got to Be a Better Way! 15 minutes
Overview
In this lesson, students will build their flexibiltiy of thinking by engaging with multiple representations. Students will search for structures that are dynamic, meaning they change in a predictable way. This is the foundation for defining functions.
Launch
Students should have their workbook, pencil, and be logged into code.pyret.org on their computer.
I Love Green Triangles
 🖼Show image
🖼Show image
I Love Green Triangles
 🖼Show image
🖼Show image
This is a fun lesson to make silly! Dramatically confess to your students, "I LOVE green triangles!" Challenge them to use the Definitions Area to code as many unique, solid, green triangles as they can in 2 minutes.
Walk around the room and give positive feedback on the green triangles. When the time is up, ask for some examples of green triangles that they wrote and copy them to the board. Be specific and attend to precision with the syntax such that students can visually spot the pattern between the different lines of code.
For example:
triangle(30, "solid", "green")
triangle(12, "solid", "green")
triangle(500, "solid", "green")
-
Is there a pattern? Yes, the code mostly stayed the same with one change each time.
-
What stayed the same? The function name
triangle, "solid", "green". -
What changed? The size of the
triangle, or the Number input. -
How many of you typed out the code from scratch each time? How many triangles were you able to code in a minute? Write this down so that you can compare to it later!!!
-
Did you know that there is a keyboard shortcut for making the previous line of code reappear in the interacions area? up-arrow
Investigate
Suppose we want to define a shortcut function called gt. When we give it a number, it makes a solid green triangle of whatever size we give it.
Select a student to act out gt. Make it clear to the class that their Name is "gt", they expect a Number, and they will produce an Image. Act out some examples before having the class add their own and record them on the board:
-
You say: gt 20! The student responds: triangle(20, "solid", "green")!
-
You say: gt 200! The student responds: triangle(200, "solid", "green")!
-
You say: gt 99! The student responds: triangle(99, "solid", "green")!
Synthesize
Thank your volunteer. Assuming they did a wonderful job, ask them:
-
How did you get to be so speedy at building green triangles? You seemed so confident! Ideally they’ll tell you that they had good instructions and that it was easy to follow the pattern
Just as we were able to give our volunteer instructions that let them take in gt 20 and give us back triangle(20, "solid", "green"), we can define any function we’d like in the Definitions Area.
Examples and Definitions
Launch
We need to program the computer to be as smart as our volunteer. But how do we do that? We already know how to do this in math!
-
Draw the table on the left below on the board.
-
We recommend starting by showing it without the equation at the bottom and talking students through the process of highlighting the variable & defining the function.
-
Once you have crowd-sourced the equation from the math side, show students how the same process of writing examples and defining the function would work in Pyret syntax.
| Math | Pyret | |
|---|---|---|
Math
|
➞ |
Pyret
|
Investigate
Have students turn to Matching Examples and Definitions (Math) (Page 26).
-
Start by looking at each table and highlighting what is changing from the first row to the following rows.
-
Then, match each table to the function that defines it.
You may also want to have students complete Matching Examples & Function Definitions (Desmos)
Now that we’ve seen how this works in math, let’s go back to gt.
400
 🖼Show image
🖼Show image
In the case of gt, the domain was a number and that number stood for the size of the triangle we wanted to make. Whatever number we gave gt for the size of the triangle is the number our volunteer inserted into the triangle function. Everything else stayed the same no matter what! We need to define gt in terms of the variable size, instead of in terms of a specific number.
Turn to Matching Examples and Function Definitions (Page 27) and look at the definition of gt in the first row of the table.
400
 🖼Show image
🖼Show image
Using gt as a model, match the mystery function examples to their corresponding definitions.
You may also want to have students complete Matching Examples & Function Definitions (Desmos) .
Connecting to Best Practices - Writing the examples is like "showing your work" in math class. - Have students circle what is changing and label it with a proper variable name. The name of the variable should reflect what it represents, such as - Writing examples and identifying the variables lays the groundwork for writing the function, which is especially important as the functions get more complex. Don’t skip this step! |
Synthesize
-
What strategies did you use to match the examples with the function definitions?
-
Why is defining functions useful to us as programmers?
Examples and Contracts
Launch
-
What is the contract for
triangle?
triangle :: Number, String, String -> Image
-
What is the contract for
gt?
gt :: Number -> Image
-
Why might someone think the domain for
gtcontains a Number and two Strings? The functiongtonly needs one Number input because that’s the only part that’s changing. The functiongtmakes use oftriangle, whose Domain is Number String String, butgtalready knows what those strings should be.
Investigate
Have students turn to Matching Examples and Contracts (Page 28).
Confirm that everyone is on the same page before moving on. You may want to have students turn to a partner, compare their findings, and discuss their thinking about anything they didn’t agree on at first.
Have students open the gt starter file (Pyret) .
-
Click Run and evaluate gt(10) in the Interactions Area.
-
What did you get back? a little green triangle!
-
Take one minute and see how many different green triangles you can make using the
gtfunction. -
Try changing one of the examples to be incorrect and click run again. What happens? The editor lets us know that the function doesn’t match the examples so that we can fix our mistake!
Have students turn to Contracts, Examples & Definitions (Page 29)
On the top half of the page you will see the contract, examples, and function defintion for gt. Using gt as a model, complete the contract, examples and function defintion for bc. Then type the Contract, Examples and Definition into the Definitions Area, click “Run”, and make sure all of the examples pass!
If you have time, have students complete
Synthesize
-
Functions can consume values besides Numbers. What other datatypes did you see being consumed by these functions?
-
Thumbs up? Thumbs to the side? or Thumbs down? How confident do you feel that you could write the contract, examples and function definition on your own if you were given a word problem about another shape function?
Additional Exercises:
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Solving Word Problems
Solving Word Problems
Students are introduced to the Design Recipe as a scaffold for breaking down word problems into chunks that will support them in writing code.
Lesson Goals |
Students will be able to:
|
|||||||||||||||
Student-Facing Lesson Goals |
|
|||||||||||||||
Materials |
||||||||||||||||
Preparation |
|
|||||||||||||||
Supplemental Resources |
||||||||||||||||
Key Points for the Facilitator |
|
|||||||||||||||
Language Table |
|
Click here to see the prior unit-based version
- contract
-
a statement of the name, domain, and range of a function
- data types
-
a way of classifying values, such as: Number, String, Image, Boolean, or any user-defined data structure
- design recipe
-
a sequence of steps that helps people document, test, and write functions
- function
-
a mathematical object that consumes inputs and produces an output
- purpose statement
-
a concise, detailed description of what a function does with its inputs
The Design Recipe 10 minutes
Overview
In this lesson students build on what they already know about multiple representations of functions (contracts, examples and definitions) to write purpose statements and gain fluency with the Design Recipe.
Launch
Have students turn to Creating Contracts From Examples (Page 32) and write contracts for the examples provided.
Investigate
You’ve started to master most of the steps of the Design Recipe, but there’s one part you haven’t seen yet: writing a purpose statement. On its own, a contract is not enough information to generate examples and write a function definition. We need to know what the function is supposed to do with what it takes in. Programmers and Mathematicians alike find it helpful to restate a problem in their own words. After all, if you can’t explain a problem to someone else, you probably don’t understand it yourself!
Turn to Writing Examples from Purpose Statements (Page 33) and read the purpose statements. What do you notice? What do you wonder?
Debrief the notice and wonder as a class. Then have students write examples that satisfy each of the contracts and purpose statements on Writing Examples from Purpose Statements (Page 33).
OPTIONAL: For more practice, have students complete Writing Examples from Purpose Statements 2.
Synthesize
What are the important elements of purpose statements? Why are purpose statements useful?
Writing Linear Functions 25 minutes
Overview
Students are given a non-working program, which uses a linear function to determine the height of a rocket after a given length of time. The "broken" code is provided to lower cognitive load, allowing students to focus on comprehension (reading the code) and making use of structure (identifying where it’s broken).
Launch
Students should have their workbook, pencil, and be logged into code.pyret.org on their computer.
Ask students to open the
rocket-height Starter File (Pyret) and click "Run". By typing start(rocket-height), they will see the simulation start to run on their computer.
Notice and Wonder What do you notice about this program? What do you wonder? |
Survey the class on their "Notices" and "Wonders" and record on the board before moving on to the discussion.
-
Is
rocket-heightworking? -
Why do you think it’s not working?
-
What do you think the purpose of this function is? How do you know?
-
What is the domain of
rocket-height? Number -
What is the range of
rocket-height? How do you know? Number, we can tell by looking at the contract for the function. -
As the program is currently written, what happens when I give the function an input of 5? 15? One million? It always returns 0.
Investigate
Let’s use the Design Recipe to fix rocket-height, and get comfortable with writing purpose statements.
Have students turn to Word Problem: rocket-height (Page 34), read the problem statement with their partner and write down the Contract and purpose statement. Then, given the contract and purpose statement, write two examples of how rocket-height should work after two different lengths of time.
-
Circle and label what’s changing in the two examples, just as you did with the green triangle function before.
-
Choose a good variable name for what’s changing.
-
Write the function definition using the variable name.
Once the Design Recipe has been completed in the workbook, students can type the code into the rocket-height program, replacing any incorrect code with their own code.
Synthesize
-
What was the problem?
-
What mistake(s) did the programmer make?
-
Where in the Design Recipe did they first go astray?
The Design Recipe allows us to trace mistakes back to the source!
More Interesting Functions flexible
Overview
For teachers who cover quadratic and exponential functions, this activity deepens students' understanding of functions and extends the Design Recipe to include those. This can also be a useful activity for students who finish early, or who need more of a challenge.
Launch
Now that rocket-height is working correctly, explore the rest of the file and try the following:
-
Remove the comment from before the
(start rocket-height)and test the program. -
Put the comment back in front of
(start rocket-height), remove the comment from(graph rocket-height), and test the program. -
Try out
(space rocket-height) -
Try out
(everything rocket-height)
Investigate
-
Can you make the rocket fly faster? Slower?
-
Can you make the rocket sink down instead of fly up?
-
Can you make the rocket accelerate over time, so that it moves faster the longer it flies?
-
Can you make the rocket blast off and then land again?
-
Can you make the rocket blast off, reach a maximum height of exactly 1000 meters, and then land?
-
Can you make the rocket blast off, reach a maximum height of exactly 1000 meters, and then land after exactly 100 seconds?
-
Can you make the rocket fly to the edge of the the universe?
Synthesize
Debrief - what did students try? Have students share their experiments with one another!
Additional Exercises:
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Structures, Reactors, and Animations
Structures, Reactors, and Animations
Students implement animation using a modified Model-View-Controller paradigm called Reactors. Using a data structure to represent the position of an object, they write draw functions to draw single frame from instances of that structure and update functions to generate new instances from previous ones. They learn how to use Reactors to combine their structure and functions into a complete animation.
Product Outcomes |
|
|||||||||||||||
Materials |
|
|||||||||||||||
Language Table |
|
- data structure
-
a datatype which packages several datatypes as fields
- field
-
a part of a data structure that has a name and holds a single value of a specified datatype
- function
-
a mathematical object that consumes inputs and produces an output
- handler
-
Connects an event (like a tick or keypress) and a function within a reactor
- instance
-
a specific, packaged value of a data structure that contains other values in its fields
- reactor
-
a value that contains a current state, and functions for updating, drawing, and interacting with that state
- state
-
the value of a changing system at any point in time (i.e. a stoplight can be in the 'red', 'yellow' or 'green' state). In Pyret, the state of a Reactor is it’s current value.
Animations in Pyret 55 minutes
Overview
Students are introduced to Reactors, Pyret’s mechanism for created animated time-based simulations or interactive programs. With Reactors serving as the bridge between making images and defining data structures, students begin to create simple animations.
Launch
You’ve learned how to create data structures, and how to create images. Now it’s time to put these together to create an animation in Pyret. We’ll even go a step further than what we did in Bootstrap:Algebra, creating an animation with movement in two dimensions.
In Bootstrap:Algebra, many decisions about your animation were made for you. We told you how many characters you had and which aspects of them could change during the animation. The danger always moved in the x-axis, the player always moved in the y-axis. In Bootstrap:Reactive, we give you much more control of your game: you decide how many characters you will have, and what aspects of them can change (position, color, size, etc). In order to have this flexibility, we need to do a little more work to set up the animation. Let’s break down an animation to see what we need.
Let’s create an animation of a sunset. The sun will start at the top-left corner of the screen and fall diagonally down and right across the sky. Here’s a running version of the animation we are trying to create. Notice that the sun dips below the horizon in the bottom-right corner.
In Bootstrap:Algebra, we talked about how an animation is made of a sequence of images that we flip through quickly. We continue to think of an animation as a sequence of images in Bootstrap:Reactive. For example, here are the first three frames of the sunset animation:
Where will we get this sequence of images? We don’t want to create them all by hand. Instead, we want to write programs that will create them for us. This is the power of computer programming. It can automate tasks (like creating new images) that might otherwise be tedious for people to do. There are four steps to creating animations programs. You’ve actually already done the first three in the first two units, but now we need to show you how to put them together.
This is a key point at which to emphasize why functions are important to computer science. Computers are good at repetition, but they need instructions telling them what steps to repeat. Functions capture those instructions.
Step 1: Define the data structure
The first step is to develop a data structure for the information that changes across frames. To do this, we need to figure out what fields our data structure will need.
Turn to Identifying Animation Data Worksheet (Page 36) in your workbook. Copy the three sunset images we gave you into the boxes at the top of the worksheet.
To identify the fields, we have to figure out what information is needed to create each frame image. Information that changes from frame to frame must be in the data structure.
On your worksheet, fill in the table just below the three images to indicate what information changes across the frames.
Hopefully, you identified two pieces of changing information: the x-coordinate of the sun and the y-coordinate of the sun. Each image also contains the horizon (the brown rectangle), but that is the same in every frame. Let’s write down a data structure that captures the two coordinates.
Fill in the second table, giving a name and type for each of the x-coordinate and y-coordinate. Then fill in the SunsetState data structure definition that we started for you at the bottom of the page. Use sunset as the name of the constructor.
You should have come up with something like this: a data block with numbers for the two coordinates.
# a SunsetState is the x-coordinate of the sun
# and the y-coordinate of the sun
data SunsetState:
| sunset(
xpos :: Number,
ypos :: Number)
endThe term state is used in computer science to refer to the details of a program at a specific point in time. Here, we use it to refer to the details that are unique to a single frame of the animation.
We have the students copy the images into the workbook partly to make sure they understand what images they are working with and partly so that they have a self-contained worksheet page for later reference.
What’s in a Name? We are adopting a convention here, in which we include "State" in the name of the data block, then use the same base name (without "State") for the constructor. By not conflating the names here, students should have an easier time distinguishing between the constructor name and data structure name. |
Any time we make a data structure, we should make some sample instances: this helps check that we have the right fields and gives us data to use in making examples later.
Investigate
At the bottom of the worksheet, use the sunset constructor to write write down the SunsetState instance for the first frame (labeled “Sketch A”). It has x-coordinate 10 and y-coordinate 300.
Step 2: Draw one frame
The second step in making an animation is to write a function that consumes an instance of one state and produces the image for that instance. We call this function draw-state. For sunset, draw-state takes a SunsetState instance and produces an image with the sun at that location (dipping behind the horizon when low in the sky). This function should use put-image, as we did with the hikers in unit 1.
Go to Word Problem: draw-state (Page 38) in your workbook and develop the draw-state function described there. Type in your function and use it (in the interactions window) to draw several individual sunset frames.
You may have noticed that we used SunsetState instead of sunset as the domain name. Remember that sunset is just the name of the constructor, while SunsetState is the name of the type. We use SunsetState whenever we need a type name for the domain or range.
We can now draw one frame, but an animation needs many frames. How can we draw multiple frames? Let’s simply the problem a bit: if you have the instance for one frame, how do we compute the instance for the next frame? Note we didn’t ask how to produce the image for the next frame. We only asked how to produce the next SunsetState instance. Why? We just wrote draw-state, which produces the image from a SunsetState. So if we can produce the instance for the next frame, we can use draw-state to produce the image.
Step 3: Produce the next frame instance
The third step in making an animation is to write a function that consumes an instance of one state and produces the instance for the next state. We call this function next-state-tick. For sunset, next-state-tick takes a SunsetState instance and produces a SunsetState instance that is just a little lower in the sky.
Go to Word Problem: next-state-tick (Page 39) in your workbook and develop the next-state-tick function described there. Use the sample SunsetState instances that you developed in step 1 as you make your examples of the function. Then, type in the code you have so far (including the data definition for SunsetState into the sunset starter file, and make sure your examples are producing the expected answers.
Together, the draw-state and next-state-tick functions are the building blocks for an animation. To start to see how, let’s first use these two functions to create the first several frames of an animation by hand (then we’ll show you how to make more frames automatically).
Run each of the following expressions in the interactions window in turn. Just copy and paste them, rather than type them by hand each time:
-
draw-state(sunset(10,300)) -
next-state-tick(sunset(10,300))
Now use draw-state on the result of next-state-tick, then call next-state-tick again:
-
draw-state(sunset(18,296)) -
next-state-tick(sunset(18,296)) -
draw-state(sunset(26,292)) -
next-state-tick(sunset(26,292))
Do you see the sun getting lower in the sky from image to image? Do you see how we are creating a “chain” of images by alternating calls to draw-state and next-state-tick? We use next-state-tick to create the instance for a new frame, then use draw-state to produce the image for that frame.
(Optional) Here’s another way to see the same sequence of expressions. Run each of the following expressions in the interactions window in turn. Just copy and paste them, rather than type them by hand each time:
-
draw-state(sunset(10,300)) -
draw-state(next-state-tick(sunset(10,300))) -
draw-state(next-state-tick(next-state-tick(sunset(10,300)))) -
draw-state(next-state-tick(next-state-tick(next-state-tick(sunset(10,300)))))
Do you see what this sequence of expressions does? Each one starts with the sun in the upper-left corner, calls next-state-tick one or more times to compute a new position for the sun, then draws the state. Notice that this sequence only has us write down one SunsetState instance explicitly (the first one). All the others are computed from next-state-tick. If we could only get Pyret to keep making these calls for us, and to show us the images quickly one after the next, we’d have an animation!
Step 4: Define an animation with a reactor
The fourth (and final) step in making an animation is to tell
Pyret to create an animation using an initial SunsetState
instance and our draw-state and next-state-tick functions. To do
this, we need a new construct called a reactor. A reactor gathers
up the information needed to create an animation:
-
An instance of the data at the start of the animation
-
(Optional) A function that knows how this data should change automatically as time passes
-
(Optional) A function that knows how to take this data and draw one frame of the animation
A reactor is designed to “react” to different events. When the
computer’s clock ticks, we’d like to call next-state-tick on the
reactor’s state, and have it update to the next state
automatically. Reactors have event handlers, which connect events
to functions.
Here, we define a reactor named sunset-react for the sunset animation:
sunset-react = reactor:
init: sunset(10, 300),
on-tick: next-state-tick,
to-draw: draw-state
endinit tells the reactor which instance to use when the program
starts. In this example, the program will start with a
SunsetState instance with the sun at (10, 30). on-tick and
to-draw are event handlers, which connect tick and draw events to
our next-state-tick and draw-state functions.
Copy this reactor definition into your sunset animation program.
Common Misconceptions
Separating the instance from the image of it is key here: when we produce an animation, we actually produce a sequence of instances, and use draw-state to produce each one. Students may need some practice to think of the instance as separate from the image that goes into the animation.
If you run your sunset program after adding the reactor, nothing seems to happen. We have set up an animation by defining sunset-react, but we haven’t told Pyret to run it. You could define multiple reactors in the same file, so we have to tell
Pyret explicitly when we want to run one.
Type interact(sunset-react) in the interactions window to run your sunset animation.
What happens when we call interact? The following diagram summarizes what Pyret does to run the animation. It draws the initial instance, then repeatedly calls next-state-tick and draw-state to create and display successive frames of your animation.
These are the same computations you did by hand in the interactions window a little while ago, but Pyret now automates the cycle of generating and drawing instances. By having functions that can generate instances and draw images, we can let the computer do the work of creating the full animation.
Functions are essential to creating animations, because each frame comes from a different SunsetState instance. The process of drawing each instance is the same, but the instance is different each time. Functions are computations that we want to perform many times. In an animation, we perform the draw-state and next-state-tick functions once per frame. Animations are an excellent illustration of why functions matter in programming.
Synthesize
Summarizing what we have seen so far, we have to write four things in order to make an animation:
-
Create a data structure to hold the information that changes across frames. This information is called the state.
-
Write a function to generate an image of the current state (we’ll call this
draw-state). -
Write a function to generate a new state from a given state (we’ll call this
next-state-tick). -
Define a {reactor} that will use an initial instance of the state and the two functions to create an animation.
At this point, you could create your own animation from scratch by following these four steps. If you do, you may find it helpful to use one of the animation design worksheets at the back of your workbook: it takes you through sketching out your frames, developing the data structure for your animation state, and writing the functions for the animation. It also gives you a checklist of the four steps above. The checklist mentions a fifth (optional) step, which involves getting your characters to respond when the user presses a key. You’ll learn how to do that in the next unit.
The animation-design worksheet is a condensed summary of the steps to creating an animation. If your students still need more scaffolding, follow the sequence of sheets that we used to develop sunset, including explicit worksheets for draw-state and next-state-tick. If your students are doing fine without the scaffolding of the design recipe worksheets, the condensed worksheet should suffice to keep them on track (though they should still write tests and follow the other steps of the design recipe as they work).
You have just seen the incredible power of functions in programming! Functions let us generate content automatically. In the early days of making cartoons, artists drew every frame by hand. They had to decide at the beginning how many frames to create. Here, we let the computer generate as many frames as we want, by letting it call next-state-tick over and over until we stop the animation. If we want to slow down the sunset, we simply change the new coordinates within next-state-tick. If we start with a larger screen size, the computer will continue to generate as many images as we need to let the sun drop out of the window. The computer can give us this flexibility as long as we provide a function that tells the computer how to generate another frame.
From Animations to Structures 55 minutes
Overview
An animation that only changes one number (e.g. - the x-coordinate of a plane flying across the sky, or the y-coordinate of a balloon floating upwards) uses that number as the Reactor state. But what if we wanted to do something more complex, which relied on keeping track of more than one number? This activity uses more complex animation to motivate the need for data structures.
Launch
 🖼Show image
You’ve learned the components of an animation in Pyret. The data structure for the state lies at the heart of the animation: each of the initial state, the
🖼Show image
You’ve learned the components of an animation in Pyret. The data structure for the state lies at the heart of the animation: each of the initial state, the draw-state function and the next-state-tick function are based on the data structure you choose. Being able to figure out the data structure you need for an animation is therefore a critical skills in making your own animations. In this lesson, we are going to practice identifying the data and creating the data structures for various animations. We will not write the entire animation. We are just going to practice identifying the data and writing the data structures.
Investigate
Exercise: Jumping Cow — Look at this animation of a cow jumping over the moon.
Go to Identifying Animation Data Worksheet (Page 36) in the workbook. Draw three frames from this animation. Choose ones that highlight differences across the frames. The frames don’t need to be consecutive.
When you chose which frames to draw, did you include ones with different images or heights of the cow? Choosing images with some variation will help you think through the data in your animation.
Fill in the table of what information changes across the frames.
In this case, the cow’s x-coordinate and y-coordinate are both changing. The image changes too, but the position (coordinates) determines which image to use. The state data structure therefore only needs to store the coordinates.
Fill in the table of what fields you need for each piece of changing information. Write a data structure CowState to capture the data in this animation.
If students want to include the image in the state, that is fine too. Examples like this are good for raising discussion about what parts of an animation depend on one another. The image doesn’t need to be in the state, but it isn’t wrong to include it there either.
 🖼Show image
Exercise: Bicycle Ride — Look at this animation of a person riding a bicycle along a street.
🖼Show image
Exercise: Bicycle Ride — Look at this animation of a person riding a bicycle along a street.
Go to the next animation worksheet page in the workbook. Draw three frames from this animation. Choose ones that highlight differences across the frames. The frames don’t need to be consecutive. Then, fill in the table of what information changes across the frames.
In this case, there are two pieces of information: the x-coordinate of the cyclist, and the angle of rotation of the bike tires.
Fill in the table of what fields you need for each piece of changing information. Write a data structure BikeState to capture the data in this animation.
 🖼Show image
Exercise: Pulsing Star — Look at this animation of a star that pulses as it moves across the sky.
🖼Show image
Exercise: Pulsing Star — Look at this animation of a star that pulses as it moves across the sky.
Go to next animation worksheet page in the workbook. Draw three frames from this animation. Choose ones that highlight differences across the frames. The frames don’t need to be consecutive.
When you chose which frames to draw, did you show the star getting smaller and then getting larger again?
Fill in the table of what information changes across the frames.
The x- and y-coordinates of the star change, as does the size of the star. These changes are easy to see across two frames. Something else changes too, but you have to look across at least three frames to see it. Imagine you had a single frame with the star at size 25. In the next frame, should the star be larger or smaller? It’s hard to tell, because we don’t know whether the star is currently in a “growing” phase or a “shrinking” one. This animation actually has a fourth state field: the direction of growth of the star. When the star is getting bigger, the star’s size should increase in the next frame. When the star is getting smaller, the size should decrease in the next frame.
Fill in the table of what fields you need for each piece of changing information. Write a data structure StarState to capture the data in this animation.
What type did you choose for the field that tracks the direction of growth? You have several choices: a boolean such as is-growing, a string such as direction (with values "grow" or "shrink"), or a number such growth-rate which is the amount to add to the size from state to state (a positive value grows the star while a negative value shrinks it). The code for next-state-tick will be cleaner if you use the number, but the others make sense before you’ve thought ahead to the code.
 🖼Show image
Exercise: Light Dimmer — Look at this animation of a slider to control the brightness of a light.
🖼Show image
Exercise: Light Dimmer — Look at this animation of a slider to control the brightness of a light.
Go to the next animation worksheet in your workbook. Draw three frames from this animation. Choose ones that highlight differences across the frames. The frames don’t need to be consecutive.
When you chose which frames to draw, did you include the far left position when the light goes out? It can be useful to think about the extreme cases when picking frames to focus on.
Fill in the table of what information changes across the frames.
In this case, we see two things changing: the y-coordinate of the slider and the brightness of the light. You could have one field for each of these. Or, you could just have a field for the y-coordinate and compute the brightness from that value (you can control the brightness of a shape by putting a number from 0 to 255 in place of "solid" or "outline" in the arguments to the shape-image functions).
Fill in the table of what fields you need for each piece of changing information. Write a data structure LightState to capture the data in this animation.
Exercise: Pong — For a real challenge of your data structure design skills, figure out the world data structure needed for a single-paddle pong game (a ball bouncing off the walls and a single user-controlled paddle). If you want to build an entire Pong game, see the optional unit on how to do this.
Closing 5 minutes
You’ve learned how to create an animation in Pyret. You’ve learned how to create a data structure for the state of your animation. You’ve written a function to draw the frame for one instance of your state data. You’ve written another function to produce the state instance for the next frame, and you’ve learned how to write a reactor to create an animation from these pieces. Your state data structures can contain information far beyond the coordinates for players: you can include images, sizes of characters, colors of elements, and so on. Once you control the data structure, you can create much richer animations than you could in Bootstrap:Algebra. Coming up, we will show you how to use keys to control your players. Later, we show you how to add other common game features to your Bootstrap:Reactive programs.
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Functions That Ask Questions
Functions That Ask Questions
Students are introduced to if-then-else expressions, writing conditionals that deal with simple types (Numbers, Strings, Booleans, etc) and data structures of their own to implement a more complex animation.
Product Outcomes |
Students learn conditional expressions by writing a simple function |
|||||||||||||||
Materials |
|
|||||||||||||||
Language Table |
|
- helper function
-
a small function that handles a specific part of another computation, and gets called from other functions
- piecewise function
-
a function that computes different expressions based on its input
What to Wear 20 minutes
Overview
Students are introduced to Pyret’s if-then-else construct.
Launch
Sometimes we want our functions to behave one way for a certain input or condition, but a totally different way for a different input or condition. Piecewise functions in mathematics also have this property (think about absolute value!). So how do we write conditionals in Pyret?
Investigate
Open the file at What to Wear. After reading through the definition for the wear function:
-
Click Run, so that you can use
wearin the interactions area. -
What does
wear(50)evaluate to? -
What does
wear(100)evaluate to? -
What is the domain and range of the
wearfunction? -
What is the name of the variable in the
wearfunction? -
Change the
wearfunction to return the shorts outfit when it’s cold (less than 30 degrees).
Synthesize
An if expression has four parts:
-
An
ifclause -
Any number of
else ifclauses -
An optional
elseclause -
An
endkeyword
The if clause has a question, followed by a : (a colon), followed by an answer for if the question evaluates to true. Each else if clause also has a question, followed by a colon, followed by an answer for if the question evaluates to true. The else: clause runs if none of the questions in the other clauses evaluated to true. It catches all the cases that aren’t covered by a specific question in one of the if or else if clauses.
The else: clause at the end of an if expression is optional. Typically, it is important to make sure your code will account for all possible conditions, and ending with else: is a useful catchall condition if all of the other conditions return false. However, this is optional in the case that every single possible condition is covered by else if statements.
At this point, we need to introduce an extension to the Design Recipe, to allow it to handle conditionals. If we look at the examples for wear, and circle everything that changes, both the input (the temperature) and the output (the image) change. However, wear only has a single variable according to the domain in its contract. Also, the image is completely dependent on the temperature — it isn’t a separate independent variable, so it wouldn’t make sense for it to be another element in the domain of wear. The fact that we have more changing things than elements in the domain tells us that wear must be a piecewise function. This is the same rule as in Bootstrap:Algebra, and just as we could in Racket, we can tell that a function must be piecewise just by looking at its contract and the examples. This helps us identify when a function we are writing in our games needs to use if, as long as we follow the Design Recipe when building it. Another way to recognize a piecewise function when looking at your examples is to note whether or not there are elements which completely depend on another. In wear, the image depends on the temperature, and does not change independently, or in response to any other changes in the function. Keep an eye out for these dependent variables in your examples as you write them to help identify piecewise functions.
This is an important point to review. Conditionals, or Piecewise functions, are a big moment in Bootstrap:Algebra, and the extension of the Design Recipe is key for students to design their own piecewise functions later on. In the next exercise, make sure they use the Recipe steps to remind them of the mechanics of this type of function.
Where’s my Order? 35 minutes
Overview
Students connect conditional functions with behaviors in games, and write one from scratch.
Launch
Let’s revisit the package delivery drone from earlier. We’re going to write a function that tells us where the package is for a given DeliveryState. This is the kind of function you might need to write later on in your game. For example, you may need to know whether a character has reached a portal at a certain part of the screen to advance to the next level, or if they’ve fallen into dangerous lava!
Investigate
 🖼Show image
Open your workbook to Word Problem: location (Page 49). Use the design recipe to write a function to tell you where the falling box is (either “road”, “house”, “delivery zone”, or “air”), based on the
🖼Show image
Open your workbook to Word Problem: location (Page 49). Use the design recipe to write a function to tell you where the falling box is (either “road”, “house”, “delivery zone”, or “air”), based on the DeliveryState.
+
Once you’ve completed the problem on paper, open the Where’s my Order? file. We’ve gotten you started with the contract and purpose statement for location in the file.
# location :: DeliveryState -> String
# Consumes a DeliveryState and produces a String
# representing the location of the box:
# either "road", "delivery zone", "house", or "air"Copy the work you have in your workbook to implement location on the computer.
In addition to writing your examples, you can also check that the location function’s behavior matches what a drawing of a DeliveryState instance shows. For example, if location returns "road" on some input, when we draw that same input, it ought to look like the package has landed in the road!
Experiment with this function!
-
Click "Run" to compile your program, then close the animation window.
-
In the interactions area, evaluate
location(START). What does it return (hopefully"air")? -
Evaluate
draw-state(START). Does it look like the box is in the air? -
Do the same for an instance of a DeliveryState where the box is in the road, on the house, and in the delivery zone.
Synthesize
These experiments show an important connection between functions that work with instances of a data structure, and the way we draw those instances. In our design for the animation, we have an understanding of what different regions of the screen mean. Here, we see that the draw-state and location functions both share this understanding to give consistent information about the animation.
Piecewise Bug Hunting 15 minutes
Overview
Students flex their conditional-function muscles, by looking at buggy conditions and figuring out what went wrong.
Launch
Investigate
Open your workbook to Syntax and Style Bug Hunting: Piecewise Edition (Page 50). In the left column, we’ve given you broken or buggy Pyret code. On the right, we’ve given you space to either write out the correct code, or write an explanation of the problems with the provided code. Work through this workbook page, then check with your partner to confirm you’ve found all the bugs!
Colorful Sun 30 minutes
Overview
Students return to an animation they’ve created before, and enhance it by using conditionals.
Launch
Let’s return to your sunset animation from the previous unit. Currently, the sun’s x and y-coordinate change to make it move across the screen and disappear behind the horizon. In this unit, we’ll make the animation a bit more realistic, by changing the color of the sun as it gets lower in the sky. At the top of the screen, the sun should be yellow, then change to orange as it gets to the middle of the screen, and then become red as it reaches the bottom, close to the horizon.
In programming, it is fairly common that you will change a program that you’ve already written to do something new or different. Modifying existing code is a valuable skill, and one that we want to practice with this exercise. It is so useful, in fact, that we’ve created a worksheet to help you map out what needs to change in an existing animation to support new behavior.
Investigate
Turn to Page 52. Fill in the description of the animation change and three sample images at the top of the first page. If you don’t have colored pencils, just make an annotation near each sketch as to what color the sun should be in that sketch.
Once you know what new behavior you want, the next task is to build it into your code. The next two tables in the worksheet ask you to think about the NEW features that are changing in your game and how you might capture them.
Talk with your partner about what new information is changing and how you might build that into your program. Does the color change in a predictable way? Is the color a new field that is independent of the fields you already have? Based on your answer, do you think you will need to add something new to your SunsetState data structure, or can you change the look of your animation based on what is already there?
There are a number of ways students can solve this problem. Once students have brainstormed with their partners, have a classroom discussion to have pairs share their ideas.
Since the color of the sun will be changing, we could add a field to the SunsetState data structure, such as a String with the current color name. However, the color will not change independently: we want the color to change based on the position of the sun in the sky, and get darker as it gets lower. Let’s figure out how to make the sun color change based only on the fields we already have.
Fill in the table at the bottom of the worksheet assuming we are not changing the data structure: which components (including existing functions) need to change?
If we have decided not to add fields, you should have marked that the draw-state method changes, but nothing else needs to. We only change next-state-tick and next-state-key if there has been a change to the data structure.
You may need to guide students to realizing that a change in the appearance of the animation can be done entirely through draw-state. This is another point for emphasizing the separation between maintaining instances and drawing instances.
How do we change draw-state? Our first instinct may be to turn it into a piecewise function, and draw something different when the SunsetState’s y-coordinate gets below 225 or below 150. This would yield code along the lines of:
fun draw-state(a-sunset):
if a-sunset.y < 150:
put-image(
rectangle(WIDTH, HORIZON-HEIGHT, "solid", "brown"),
200, 50,
put-image(circle(25, "solid", "yellow"),
a-sunset.x, a-sunset.y,
rectangle(WIDTH, HEIGHT, "solid", "light-blue")))
else if a.sunset.y < 225:
# same code with "orange" as sun color
else:
# same code with "red" as sun color
end
endNotice that this version contains three very similar calls to put-image. The only thing that is different about these three calls is the color we use to draw the sun. Whenever you find yourself writing nearly-identical expressions multiple times, you should create another function that computes the piece that is different. You can then write the overall expression just once, calling the new function to handle the different part. Functions that handle one part of an overall computation are called helper functions.
Assume for the moment that we had written a helper function called draw-sun that takes a SunsetState and returns the image to use for the sun. If we had such a function, then our draw-state function would look as follows:
fun draw-state(a-sunset):
put-image(
rectangle(WIDTH, HORIZON-HEIGHT, "solid", "brown"),
200, 50,
put-image(draw-sun(a-sunset),
a-sunset.x, a-sunset.y,
rectangle(WIDTH, HEIGHT, "solid", "light-blue")))
endOpen your workbook to Word Problem: draw-sun (Page 53). Here we have directions for writing a function called draw-sun, which consumes a SunsetState and produces an image of the sun, whose color is either “yellow”, “orange”, or “red” depending on its y-coordinate.
The word problem assumes a background scene size of 400x300 pixels. Once students use their draw-sun function in their animation, they may need to change the specific conditions if they have a much larger or smaller scene.
Once you’ve completed and typed the draw-sun function into your sunset animation program, modify draw-state to use it as we showed just above.
Now let’s think about having the sunset animation "`start again`"after the sun sets, with the sun reappearing in the upper-left corner.
Assume you edited your animation to restart the sun at the upper left after it sets. What color should the sun be when it appears at the upper-left the second time around? What color will it be based on your code? Will it be yellow again, or will the color have changed somehow to red?
To figure this out, think about what controls the color of the sun in your current code.
Edit the sunset animation so that the animation restarts.
-
Which of your functions has to be modified to include this change?
-
Is restarting fundamentally about drawing one frame or about generating new instances?
-
Use that question to help yourself figure out which function to modify. You could use the space for examples of functions at the end of your worksheet on extending the animation to write a new example before you modify your code.
Synthesize
This question about the color of the sun is an especially good question-and it likely to come up-from students who may have experience programming with variables and updates in other languages, such as Scratch (where the color would have changed to red). In our approach, where we simply determine the sun color from the y-coordinate, the sun should naturally restart as yellow. Of course, if students had maintained the sun color as a separate field in their data structure, they would have to consider this issue, and manually reset the sun color as well as the y-coordinate when restarting the animation.
Optional: In addition to changing the color of the sun, have the background color change as well: it should be light blue when the sun is high in the sky, and get darker as the sun sets.
Like changing the color of the sun, there are multiple valid ways of completing this optional activity. If you have students solving the same problem with different code, have them share their code with the class and have a discussion about the merits of each version.
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Key Events
Key Events
Students are introduced to key events, and use if-then-else expressions to write a key-event handler that moves an image left and right as part of an interactive animation.
Product Outcomes |
|
|||||||||||||||
Materials |
|
|||||||||||||||
Language Table |
|
- event
-
something that happens outside of a running program, which the program can respond to
- handler
-
Connects an event (like a tick or keypress) and a function within a reactor
- reactor
-
a value that contains a current state, and functions for updating, drawing, and interacting with that state
2D Character Movement 45 minutes
Overview
Students learn about events, and add key-event handling to their games.
Launch
We’ve already seen one kind of interactivity in our programs: getting the next state from the current state on a tick-event. This is perfect for animations that happen on their own, without any user intervention. In a game, that might be clouds moving across the sky or a ball bouncing on its own. An important kind of behavior in interactive programs is to respond user input, such as keypresses. A keypress, like the tick of a clock, is a kind of event, and we’ll re-use the idea of an event handler like on-tick and a function like next-state-tick. For key-events, the event handler is called on-key, and our function next-state-key will compute the next state from the current one after a key event. We’re going to use this idea to build up a reactor with a character moving in two dimensions, where the movement is triggered by keypresses.
Open up the Moving Character Starter File.
It contains a data block for representing a character’s position (CharState) that has an x and y position.
Write an example instance of a CharState where both the x field and the y field are between 100 and 500. Give it the name middle. We’ve filled in a picture of Sam the Butterfly from Bootstrap:Algebra. There is a drawing function called draw-state provided that simply draws the character image on a white background at the x and y coordinate in a CharState.
Run the program, and use draw-state to draw the example instance you created above. Did it appear where you expected?
This is a reminder that it’s often useful, when working on programs that use data to represent positions in an image, to make sure we understand what values in the data structure correspond to which drawing behavior.
Write an example instance that represents the butterfly in the top-right corner of the window. Give it a meaningful name of your own choice. Re-run the program, and check using draw-state that it showed up where you expect.
There is also a contract for a function next-state-key, which looks like:
# next-state-key :: CharState, String -> CharState
# Moves the character by 5 pixels
# in the corresponding direction
# if an arrow key ("up", "left", "down", or "right")
# is pressed, & leaves the character in place otherwiseHow does the contract of next-state-key differ from the contract of next-state-tick in your previous programs?
It is different from the contract for next-state-tick (which handles tick events) in an important way. When a key event happens, the next state may differ depending on which key was pressed. That means the next-state-key function needs both the current state and which key was pressed as parts of its domain. That’s why next-state-key has an additional String input, which represents the key pressed by the user.
Create an example instance that corresponds to the position 5 pixels to the right of the example instance you wrote above. Use draw-state to check it, as before.
This gives us a good input and output test for the examples block when working on next-state-key. What call to next-state-key should connect these two example instances?
Investigate
Use the Design Recipe to fill in your examples and definition of next-state-key. Use the sample instances you created before in the examples block.
It’s an important point that next-state-key takes in an extra piece of information: the pressed key. This makes it much richer in terms of its purpose statement, which should describe what different keys ought to do to the state of the reactor. Students will create something like this completed file by adding a next-state-key function
Once you’ve implemented next-state-key, experiment with it in the interactions area:
-
Try
draw-state(next-state-key(middle, "left")). How is the output different fromdraw-state(middle)? -
Try using a few different calls to
next-state-keyto move the character several times, then draw it. For example:draw-state(next-state-key(next-state-key(middle, "left"), "up"))
As with tick-events, we can manually pass keypress strings into this function, see what the next state would be, and even draw that state to see what it looks like. That’s great, but we still want to hook this function up to a reactor, so that it actually handles keypresses from a user playing the game. To do this, we need to create a reactor use on-key to specify that our next-state-key function should be called when the user presses a key (we don’t need to specify an on-tick handler, since for now the only movement in our program comes from keypresses). Our reactor with a to-draw and on-key handler looks like this:
char-react = reactor:
init: middle,
to-draw: draw-state,
on-key: next-state-key
endMake your program create a reactor by that uses the on-key handler with the next-state-key function you just implemented. Run the program and use interact(char-react) to start the reactor. Does it work the way you expected? If it doesn’t, check:
-
Does the program have any typos or syntax errors?
-
Do the examples of
next-state-keymatch what you expect, creating a newcharinstance with appropriate x and y values? -
Do the examples pass the implementation of
next-state-key? -
Did you remember to add
on-keyto the reactor? -
Did you remember to re-run the program and use
interactto start the animation?
With this working, you can see the behind-the-scenes work that was going on in Sam the Butterfly from Bootstrap:Algebra. To get to the same point as in Bootstrap:Algebra, we’d next implement is-onscreen to check if Sam has left the board, and use it in next-state-tick.
Synthesize
Act out a reactor with key-events. You will need four students: one who acts as the next-state-key function, one who acts as the keyboard (you could also have the class act as a keyboard by having students shout out keys), one who acts as the reactor, and one who acts as the draw-state function. Give each student a few sheets of paper and something to write with.
When a key is "pressed" by the keyboard, the reactor write the current state and the key that was pressed, then shows their paper to next-state-key. next-state-key produces a new state based on the current state and the key, writes it down, and then hands the new state back to the reactor. The reactor discards their old state, replacing it with the new one, and shows the new one to draw-state. draw-state produces an image for the reactor to post, and draws it on paper. They hand the image to the reactor, who holds it up as the new frame in the animation. We recommend not having a next-state-tick function for this activity, to keep the focus on key events. You can add a on-tick handler in a separate stage when talking through games which have both time- and key-based events.
Optional: implement boundaries to keep character onscreen, using the same ideas as safe-left and safe-right from before. You can also write safe-top and safe-bottom, and use all of them to keep the character fully on the screen.
Optional: use num-to-string and text to display the position at the top of the window.
Combining Ticks and Keypresses 45 minutes
Overview
This activity introduces students to Reactor programs that use key-events and tick events. Students create a "digital pet", which responds to key commands but also changes state on its own.
Launch
Now, you’ve seen how to use functions to compute the next state in a game or animation for both tick and key events. We can combine these to make an interactive “digital-pet” from scratch!
Open the Virtual Pet Starter file. Run it. You will see a frame come up, showing a cat face and green status bars for the cat’s sleep and hunger.
Notice that not much is happening! To make this game more interesting, we want to add three behaviors to it:
-
as time passes, the hunger and sleep values should decrease
-
a human player should be able to increase hunger and sleep through keypresses
-
the image of the cat should change when hunger and sleep both reach 0 (and the player loses the game)
Investigate
In this lesson, you will extend the animation three times, once for each of these behaviors, by adding or changing the functions that make up an animation. To do this, you will use the Animation Extension Worksheet three times. Note that none of these should require adding any new fields to the data definition, just adding and editing functions like next-state-tick, next-state-key, and draw-state. We will walk you through the first use of the animation extension worksheet, then let you try the other two on your own.
Extension 1: Decrease Hunger and Sleep on Ticks
For this extension, we want to decrease the hunger by 2 and the sleep by 1 each time the animation ticks to a new frame.
Open your workbook to Animation Data Worksheet (Page 55) and Page 56, which shows you the extension worksheet filled in for this extension.
In this filled-in worksheet, the description from the problem is written down into the "goal" part of the worksheet. This is like the “purpose statement” for the feature.
Think about what sketches you would draw to illustrate the animation with this new behavior. Then check out the ones we drew on the example worksheet. Notice that they focus on the bars having different lengths.
Next, we consider the tables that summarize what now changes in the animation.
What changes between frames now that didn’t in the starter file for the virtual pet?
The worksheet identifies that both hunger and sleep are changing in new ways. Since they aren’t new fields, this feature is completely dependent on existing data, and we don’t need to add any new fields. We therefore leave the second table empty (since we aren’t adding new fields).
Next, we identify the components that we need to write or update. We don’t need to change the data definition at all, because no new fields were added. We may need to update draw-state function, since the size of the bars changes. We definitely need to write the next-state-tick function, which doesn’t yet exist. We do not need to address anything about keypresses with this feature, so next-state-key is untouched. Since next-state-tick has been added for this feature, we need to add a on-tick handler to the reactor.
Now that we’ve planned what work needs to be done (on paper), we can start thinking about the code. As always, we write examples before we write functions, so we are clear on what we are trying to do.
Come up with two example instances of PetState that illustrate what should happen as we change the sleep and hunger fields. You can see the ones we chose on the worksheet. What’s another good example for us to use in coding and testing?
In our samples, we estimate a bit from looking at the pictures, but note that we pick numbers that would work with the desired behavior — MIDPET represents the state after 25 ticks, because hunger is 50 less (decreased by 2 each tick), and sleep is 25 less (decreased by 1 on each tick). The LOSEPET sample instance corresponds to the state when both hunger and sleep values are 0.
Use your sample instances to write examples of the next-state-tick function, which we marked as a to-do item on the first page of the worksheet.
Now we need to use this information to edit the current code, checking off the boxes we identified as we go.
Look at the draw-state function: how will it need to change to draw boxes for the sleep and hunger values?
The draw-state function already does this, so we can check the draw-state changes off as being done (without doing additional work).
Develop next-state-tick, using the contract in the starter file and the examples from the worksheet.
Once we’ve finished using the design recipe to implement next-state-tick, we can check off its box. Finally, we need to add the handler to the reactor so the reactor calls the function we just wrote on tick events.
Edit the pet-react reactor to include next-state-tick alongside the on-tick handler.
You should have ended up with something like this:
pet-react = reactor:
init: FULLPET,
on-tick: next-state-tick,
to-draw: draw-state
endMake sure you get a working animation with bars that decrease before moving on, like this:
Modification 2: Key Events
Next, we’ll add key events to the game so the player can increase them so they don’t reach zero!
Turn to Animation Data Worksheet (Page 57) and Page 58 in your workbook. Fill in the first page to plan out the following extension: On a keypress, if the user pressed “f” (for “feed”), hunger should increase by 10. If the user pressed “s” (for “sleep”), sleep should increase by 5. If the user presses any other keys, nothing should change.
As you fill in the worksheet, think about useful sketches that capture this new feature, whether you need new fields, and which functions are effected.
When you’ve implemented next-state-key, you can add it to the reactor at the bottom of the file with:
pet-react = reactor:
init: FULLPET,
on-key: next-state-key,
on-tick: next-state-tick,
to-draw: draw-state
endand test out your game!
Modification 3: Change Pet Image When Game is Lost
When any bar reaches zero, the game is lost and your pet is sad — make the picture change to show the player this! In addition, when the game is lost, the “f” and “s” keys shouldn’t do anything. Instead, the user should be able to press the “r” key (for “restart”), to reset hunger and sleep 100, and start playing again. Use the an animation-extension worksheet to plan out your changes.
Synthesize
You now know everything you need to build interactive games that react to the keyboard, draw an image, and change over time! These are the fundamentals of building up an interactive program, and there are a lot of games, simulations, or activities you can build already. For example, you could build Pong, or the extended Ninja Cat, a more involved Pet Simulator, a game with levels, and much, much more.
Some of these ideas are more straightforward than others with what you know. The rest of the workbook and units are designed to show you different features that you can add to interactive programs. You can work through them all if you like, or come up with an idea for your own program, and try the ones that will help you build your very own program!
Additional Exercises
-
Find your own images to create a different virtual pet Stop the bars from overflowing some maximum (produce something like this completed game).
-
Add an
x-coordto thePetStateso the pet moves around, either on keypress or based on clock ticks. -
Add a
costumeto thePetState, then change the draw-pet function so that it changes the costume based on the pet’s mood (if a-pet.hunger <= 50, show a picture of the pet looking hungry)
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Refactoring
Refactoring
This lesson focuses on code quality. Starting from a working program, students refactor the code to be more readable, writing helper functions thinking structurally about a complex program.
Product Outcomes |
|
|||||||||||||||
Materials |
||||||||||||||||
Language Table |
|
- refactor
-
the process of changing the style or structure of a program’s code, without changing the program’s behavior
Refactoring - a Case Study 40 minutes
Overview
Student are introduced to the programming concept of refactoring, which closely models the Mathematical Practice 7: Identify and make use of structure. Students create an emoji generator, and then refactor it to make the code cleaner.
Launch
One of the most common tasks software developers find themselves performing is refactoring code. This means taking code that is already working and complete, and cleaning it up: adding comments, removing unnecessary expressions, and generally making their code more readable and useable by others. Refactoring does not change the behavior of the program, only the appearance of the code. For instance, a messy expression like:
(((4 * 4) + (3 / (8 - 6))) * (9 * 9)) * (1 + 1)could be refactored into:
((num-sqr(4) + (3 / 2)) * num-sqr(9)) * 2Both expressions return the same value, but the second is much more readable. Refactoring can involve using existing functions (such as num-sqr in the example above) or writing new functions to perform small tasks.
Open the Robot Emoji file and press "Run". In this file, there are two versions of the same program written by different students.
Take a look at the definitions in this file, and, with your partner, discuss what you notice. Which student’s code is easiest to read and understand? Which formatting do you like better? If you were collaborating on a project with another programmer, which version of this code would you rather to receive, and why?
Discuss with students the differences in documentation, formatting, and organization of the two versions of the emoji code.
Next, we’re going to practice refactoring an existing program that draws an image.
Investigate
Open the Emoji Refactoring file and click "Run".
This code draws an image of a simple face emoji. Without changing the final image produced, can you see any opportunities to edit the code to make it more readable?
Refactor the code provided. This could include adding comments, more space betwen expressions, or simplifying the existing expressions. Once finished, write one more expression to create a smaller (emoji-sized) version of the original image.
This activity can be done individually or as a class, with students giving suggestions for refactoring code projected at the front of the room. Once the refactoring is completed, students can practice using image functions to create an emoji of their own.
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Your Own Drawing Functions
Your Own Drawing Functions
This lesson removes earlier scaffolding from working with Reactors, having students brainstorm an original animation of their own and implement it from start-to-finish. This requires them to plan out what kind of data structure they will need, and how it will be drawn and updated.
Product Outcomes |
|
|||||||||||||||
Materials |
||||||||||||||||
Language Table |
|
Drawing with a Single Number 30 minutes
Overview
Students practice writing a simple function to draw the state of a Reactor, when that state consists of only a single number.
Launch
The majority of reactive programs you’ll write in this course will use data structures consisting of multiple pieces of data, whether that be Numbers, Strings, Images, or Booleans. However, it’s not required to have a full data structure in order to use a reactor. In fact, we can create an animation based on just a single number!
Open the Blank Single Number draw-state file and take a look at the code. Before hitting "Run", can you guess what this code will do?
include image
include reactors
# next-state-tick :: Number -> Number
fun next-state-tick(n):
n + 1
end
# draw-state :: Number -> Image
fun draw-state(n):
"fix me!"
end
num-react = reactor:
init: 1,
# to-draw: draw-state,
on-tick: next-state-tick
end
interact(num-react)Notice how there is no data block in this file. Both the next-state-tick and the draw-state function consume a single number, and the initial value given to the reactor is also a single number (in this case, 1.)
Click Run. What do you see?
According to the next-state-tick function, on every clock tick the state (a single number) will increase by one, which is exactly what happens. Since we didn’t tell the reactor how to draw the state (the to-draw part of the reactor is commented out), when the reactor runs we see the state of the reactor (a single number) increasing, instead of an animation.
What do you think would happen if we had a reactor with a complete draw-state function, but a next-state-tick function that never updated the state? (Consuming and producing the same value.)
Reinforce the fact that, although the draw-state and next-state-tick functions work together within a reactor to produce an animation, each function can work without the other. In this example, next-state-tick will update the state even without a function to draw the state.
There are much more interesting things we can display using a number as the state of the reactor, however!
Investigate
Change the draw-state function so that it consumes a Number and produces an image. Then, uncomment the to-draw: draw-state line in the reactor to see an animation when the program runs!
Encourage students to brainstorm and share ideas for the draw-state function before beginning. Some possible options include:
-
Drawing a star of size n (so that it gets larger on each tick)
-
Display n as an image using the text function.
-
Have students share back the draw-state functions they wrote.
Drawing with Two Numbers 30 minutes
Overview
This activity turns up the cognitive load: students practice writing a function to draw the state of a Reactor, when that state consists of a structure containing two numbers.
Launch
You’ve practiced writing a draw-state function using a single number as a state, now let’s look at something a bit more familiar.
Open the Blank 2 Number draw-state file and take a look at the code.
include image
include reactors
data AnimationState:
| state(
a :: Number,
b :: Number)
end
START = state(1, 100)
# next-state-tick :: AnimationState -> AnimationState
fun next-state-tick(s):
state(s.a + 1, s.b - 1)
end
# draw-state :: AnimationState -> Image
fun draw-state(s):
"fix me!"
end
state-react = reactor:
init: START,
# to-draw: draw-state,
on-tick: next-state-tick
end
interact(state-react)This code includes a data structure (called AnimationState) containing two numbers as its fields, a and b. As before, the draw-state function is incomplete, and commented out from the reactor.
Based on the next-state-tick function defined here, what do you think will happen when you hit ‘Run’? Discuss with your partner, then try it out!
With only the next-state-tick function, we can see the state updating, increasing the first number by 1 and decreasing the second number by 1 each tick.
Investigate
How could you define a draw-state function to show something interesting when the program runs? Branstorm with your partner, then change the existing, broken draw-state function to consume an AnimationState and produce an image. Then, comment out the to-draw: draw-state line in the reactor to see an animation when the program runs!
Some possible ideas for this activity:
-
Display two shapes of size a and b, which get larger and smaller, respectively, as the reactor runs.
-
Make a and b the coordinates of an image, moving down and to the right across a background as the reactor runs.
Synthesize
Have students share back what they brainstormed before beginning, then share the completed draw-state functions they wrote, and the animations they created!
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Build Your Own Animation
Build Your Own Animation
Students create a game of their own design using what they have learned so far.
Product Outcomes |
|
|||||||||||||||
Materials |
|
|||||||||||||||
Language Table |
|
- instance
-
a specific, packaged value of a data structure that contains other values in its fields
Build Your Own Animation 55 minutes
Overview
Students apply the Animation Design worksheet to their own, creative animations.
Launch
You’ve now learned the core tasks that go into building an animation:
-
Draw some sketches to illustrate your animation
-
Analyze the game elements to identify the information that changes across frames
-
Create a data structure to capture those elements
-
Write
draw-stateand one or both ofnext-state-tickandnext-state-key -
Create a reactor to pull it all together
In this lesson, we show you how to use our Animation Design Worksheet to keep track of these steps as you build your own animation.
Brainstorm an animation or game that you would like to build. Don’t make it too complicated. Start with no more than 4 pieces of changing information.
As we saw in the previous unit, we can always go back and add more elements or details to an existing animation. So keep it simple to get a basic game running, then you can add more later.
Turn the Animation Design Worksheet on Page 41 in your workbook.
Fill in three sketches from your animation. Discuss with your partner whether the sketches you chose have highlighted interesting aspects of your game.
The tables below the animation sketches ask you to identify the elements in your game.
Fill in the first table, noting the elements that are changing and how they are changing. If you have more things changing than there are rows, consider making a simpler animation first then extending (at the end of the lesson).
Have your partner or a classmate check your work — make sure you both agree that you’ve identified everything that is changing.
Fill in the second table, figuring out data types that capture each piece of information that is changing in your animation. Talk with someone to check your work (and help check the work of others).
The table at the bottom of the worksheet asks you to make a to-do list of which functions and components you will need to write to build your animation.
Mark off which components and functions you expect to need. Think about whether your animation updates on ticks, key presses, or both.
Students should have ended up checking "sample instances", draw-state, and "reactor", plus one or both of next-state-tick and next-state-key. Sample instances get created anytime you have to create a data structure, and every animation or game has an underlying data structure.
Go to the top of the second page of the worksheet.
Investigate
Define a data structure for your game state, with one field for each piece of changing information that you identified in the table of the middle of page 1 of the worksheet. The name of your data structure is up to you, but should reflect the theme of your game (like RocketState, SoccerState, OceanState, etc)
Is your data structure defined?
Write down the sample instances of your data structure for each sketch that you drew at the top of the first page of the worksheet.
At this point, you could open a new Pyret file and type in your data structure and your sample instances. This would help you check whether your instances and data block are consistent with each other. If you don’t have access to the computer right now, you can come back and do this step later.
Sanity-checking each bit of code and examples as you go helps students catch errors early. So typing their work so far in now makes sense, if your class set up allows it.
Now you have to develop whichever functions you marked off on the todo-list on the bottom of page 1 of the worksheet.
Pick one of the functions you need to develop. Follow the design recipe, including working out examples, as you develop each function. Finish and test each function before moving onto the next one.
There are extra design-recipe worksheets in the back of the workbook if you need them to help you remember the steps (domain and range, examples, function, and typing and testing your function).
You need to decide how much scaffolding and help your students need at this point. You can feel free to let them work on their own, or you can encourage them to work through design-recipe worksheets if they still need the structure that those provide. The main goal is to have students tackle only one function at a time, and to make sure it is working before they go on to the other functions.
Finally, we can build and run the animation by defining a reactor.
Add a reactor to your file, then interact with it to run your animation!
Remember that a reactor looks like:
??? = reactor:
init: ???,
on-key: next-state-key,
on-tick: next-state-tick,
to-draw: draw-state
endwhere you replace the ??? with names and instances that correspond to your game.
Closing
Congratulations! You have created your own animation from scratch. If there are features you want to add, use the extra Animation Extension Worksheets from the back of the workbook to help plan and manage your changes. If you build up an animation one piece at a time, you can get to a fairly complex game in a manageable way.
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Adding Collisions
Adding Collisions
Students use the distance formula and their data structures to determine when two or more characters in their games have collided. They extend their update handlers to generate a new structure that represents the game after a collision has occurred.
Product Outcomes |
|
|||||||||||||||
Materials |
|
|||||||||||||||
Language Table |
|
- helper function
-
a small function that handles a specific part of another computation, and gets called from other functions
- hypotenuse
-
the side opposite the 90-degree angle in a right triangle
The Distance Formula 30 minutes
Overview
Students implement the distance formula, to prepare for collision detection in their games.
Launch
So far, none of the animations we’ve created included any distance or collision-detection functions. However, if you want to make a game where the player has to hit a target, avoid an enemy, jump onto platforms, or reach a specific part of the screen, we’ll need to account for collisions. This is going to require a little math, but luckily it’s exactly the same as it was in Bootstrap:Algebra.
image
-
In the image above, how far apart are the cat and dog?
-
If the cat was moved one space to the right, how far apart would they be?
-
What if the cat and dog switched positions?
Finding the distance in one dimesion is pretty easy: if the characters are on the same number line, we subtract the smaller coordinate from the larger one, and we have our distance.
When the cat and dog were switched, did you still subtract the dog’s position from the cat’s, or subtract the cat’s position from the dog’s? Why?
Unfortunately, most distances aren’t only measured in one dimension. We’ll need some code to calculate the distance between two points in two dimensions.
Investigate
-
How could you find the distance between the two points shown in this image?
-
How could you find the length of the C, also called the Hypotenuse?
Let’s start with what we do know: if we treat the x- and y-intercepts of C as lines A and B, we have a right triangle.
What is the line-length of A? Would it be different if the triangle pointed downward, and intercepted the point (0, −4)?
Ancient civilizations had the same problem: they also struggled to find the distance between points in two dimensions. Let’s work through a way to think about this problem: what expression computes the length of the hypotenuse of a right triangle?
For any right triangle, it is possible to draw a picture where the hypotenuse is used for all four sides of a square. In the diagram shown here, the white square is surrounded by four gray, identical right-triangles, each with sides A and B. The square itself has four identical sides of length C, which are the hypotenuses for the triangles. If the area of a square is expressed by side ∗ side, then the area of the white space is C^2.
By moving the gray triangles, it is possible to create two rectangles that fit inside the original square. While the space taken up by the triangles has shifted, it hasn’t gotten any bigger or smaller. Likewise, the white space has been broken into two smaller squares, but in total it remains the same size. By using the side-lengths A and B, one can calculate the area of the two squares.
What is the area of the smaller square? The larger square?
image
The smaller square has an area of A^2, and the larger square has an area of B^2. Since these squares are just the original square broken up into two pieces, we know that the sum of these areas must be equal to the area of the original square:
A^2 + B^2 = C^2
Does the same equation work for any values of A and B?
To get C by itself, we take the square-root of the sum of the areas:
√( A^2 + B^2 ) = C
Pythagoras proved that you can get the square of the hypotenuse by adding the squares of the other two sides. In your games, you’re going to use the horizontal and vertical distance between two characters as the two sides of your triangle, and use the Pythagorean theorem to find the length of that third side.
Remind students that A and B are the horizontal and vertical lengths, which are calculated by line-length.
-
Turn to Page 45 of your workbook - you’ll see the formula written out.
-
Draw out the circle of evaluation, starting with the simplest expression you can see first.
-
Once you have the circle of evaluation, translate it into Pyret code at the bottom of the page, starting with
check: distance(4, 2, 0, 5) is... end
Now you’ve got code that tells you the distance between the points (4, 2) and (0, 5). But we want to have it work for any two points. It would be great if we had a function that would just take the x’s and y’s as input, and do the math for us.
-
Turn to Page 46, and read the problem statement and function header carefully.
-
Use the Design Recipe to write your distance function. Feel free to use the work from the previous page as your first example, and then come up with a new one of your own.
-
When finished, type your
distancefunctions into your game, and see what happens. -
Does anything happen when things run into each other?
You still need a function to check whether or not two things are colliding.
Watch Out! Pay careful attention to the order in which the coordinates are given to the distance function. The player’s x-coordinate (px) must be given first, followed by the player’s y (py), character’s x (cx), and character’s y (cy). Just like with making data structures, order matters, and the distance function will not work otherwise. Also be sure to check that students are using num-sqr and num-sqrt in the correct places. |
Collision Detection 30 minutes
Overview
Students implement a simple Boolean-producing function, which composes with the distance function they implemented.
Launch
So what do we want to do with this distance?
How close should your danger and your player be, before they hit each other?
At the top of Page 47 you’ll find the Word Problem for is-collision.
-
Fill in the Contract, two examples, and then write the code. Remember: you WILL need to make use of the
distancefunction you just wrote! -
When you’re done, type it into your game, underneath
distance.
Now that you have a function which will check whether two things are colliding, you can use it in your game! For extra practice, You can also implement collision detection into this Pyret Ninja Cat game. This is the program we’ll be altering for this lesson, as an example. In Ninja Cat, when the cat collides with the dog, we want to put the dog offscreen so that he can come back to attack again.
Investigate
Out of the major functions in the game (next-state-tick, draw-state, or next-state-key), which do you think you’ll need to edit to handle collisions, changing the GameState when two characters collide?
We’ll need to make some more if branches for next-state-tick.
-
Start with the test: how could you check whether the cat and dog are colliding? Have you written a function to check that?
-
What do the inputs need to be?
-
How do you get the
playeryout of theGameState?playerx? -
How do you get the
dangerxout of theGameState?dangery?
if is-collision(
g.playerx,
g.playery,
g.dangerx,
g.dangery): ...result...Remember that next-state-tick produces a GameState, so what function should come first in our result?
if is-collision(
g.playerx,
g.playery,
g.dangerx,
g.dangery):
game(
...playerx...,
...playery...,
...dangerx...,
...dangery...,
...dangerspeed...
...targetx...
...targety...
...targetspeed...)And what should happen when the cat and dog collide? Can you think of a number that puts the dog off the screen on the left side? What about the dog’s y-coordinate? We could choose a number and always place it at the same y-coordinate each time, but then the game would be really easy! To make it more challenging, we’d like the dog to appear at a random y-coordinate each time it collides with the cat. Thankfully, Pyret has a function which produces a random number between zero and its input:
# num-random :: Number -> Number
if is-collision(
g.playerx,
g.playery,
g.dangerx,
g.dangery):
game(
g.playerx,
200,
num-random(480),
0,
0,
g.targetx,
g.targety,
g.targetspeed)Collision detection must be part of the next-state-tick function because the game should be checking for a collision each time the GameState is updated, on every tick. Students may assume that draw-state should handle collision detection, but point out that the Range of draw-state is an Image, and their function must return a new GameState in order to set the locations of the characters after a collision.
Once you’ve finished, write another branch to check whether the player and the target have collided. Challenges:
-
Change your first condition so that the danger gets reset only when the player and danger collide AND the cat is jumping. (What must be true about the player’s y-coordinate for it to be jumping?)
-
Add another condition to check whether the player has collided with the danger while the player is on the ground. This could be a single expression within
next-state-tick, or you can write a helper function calledgame-overto do this work, and use it in other functions as well (maybe the GameState is drawn differently once the game is over.)
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Scoring
Scoring
Students extend the data structure that represents their game to include a score, then modify their helper functions and event handlers to update and display that score.
Product Outcomes |
|
|||||||||||||||
Materials |
||||||||||||||||
Language Table |
|
- helper function
-
a small function that handles a specific part of another computation, and gets called from other functions
Adding a Scoring System 45 minutes
Overview
Students add a score to their game.
Launch
The score is something that will be changing in the game, so you can be sure that it has to be added to the ____State data structure. In our example Ninja Cat program, we’ve called our structure GameState, which currently contains the x and y-coordinates for our player, danger, and target, plus the speed of the danger, and speed of the target. Your game(s) will likely have different structures.
Investigate
-
What data type is a score? Number, String, Image, or Boolean?
-
What would be the score in your starting game state? (we called this
STARTin our game.) -
Change the data structure in your game so it includes a score.
Remember: Since your structure is changing, you now have to go through your game code — every time you call the constructor function for your structure (ours is game()), the score must be included. It may be helpful to add the score as the very first or last field of the structure, to make this easier.
How would you get the score out of one of your instances?
The GameState structure for our Ninja Cat game now looks like this:
data GameState:
game(
playerx :: Number,
playery :: Number,
dangerx :: Number,
dangery :: Number,
dangerspeed :: Number,
targetx :: Number,
targety :: Number,
targetspeed :: Number,
score :: Number)
endReminder Your students will likely have radically different games at this point in the course. This lesson is not meant to be followed exactly, but rather used to give students an idea of what steps they should take to add a scoring system to their own games. For extra practice, students can work through adding a scoring system to the Ninja Cat program as well as their own games. |
Now that the game has a score, that score needs to actually increase or decrease depending on what happens in the game. For our Ninja Cat game, we’ll say that the score should go up by 30 points when Ninja Cat collides with the ruby (target), and down by 20 points when she collides with the dog (danger).
-
Which of the
ifbranches in yournext-state-tickfunction checks whether your player has collided with another character? -
How would you decrease the game’s
scoreby 20 points if the player collides with the danger? -
Hint: How many dangers does your game have? If there are multiple things your player could hit to lose points, remember to check for each possible collision condition!
If you completed the optional challenge at the end of the Collisions Feature to write the function game-over, you already have your own helper function to check whether or not your game over condition is met. That will be the first condition inside next-state-tick, since we don’t want the game to continue if it’s already over! (In our Ninja Cat game, game-over returns true if the cat collides with the dog, AND the cat is on the ground.) After checking whether or not the game is over, the next three conditions in our next-state-tick function check whether the player has collided with the danger and target, as well as whether the player is jumping on the danger:
# next-state-tick :: GameState -> GameState
fun next-state-tick(g):
if game-over(g): g
# if player and danger collide while player is on the ground,
#reset player and danger and decrease score
else if is-collision(g.playerx, g.playery, g.dangerx, g.dangery)
and (g.playery < 110):
game(
START.playerx,
START.playery,
750,
g.dangery,
g.dangerspeed,
g.targetx,
g.targety,
g.targetspeed,
g.score - 20)
# if player and danger collide while player is jumping,
# reset danger and increase score
else if is-collision(g.playerx, g.playery, g.dangerx, g.dangery)
and (g.playery > 110) and (g.playery < 300):
game(
g.playerx,
200,
-100,
0,
0,
g.targetx,
g.targety,
g.targetspeed,
g.score + 30)
# if player and target collide, reset target and increase score
else if is-collision(g.playerx, g.playery, g.targetx, g.targety):
game(
g.playerx,
g.playery,
g.dangerx,
g.dangery,
g.dangerspeed,
-400,
0,
0,
g.score + 30)Change your own game code so that your score increases and decreases depending on various game conditions: Maybe your score increases when the player collides with a target, reaches a specific area of the screen, or reaches a specific area only after picking up an item. Maybe your game’s scoring system isn’t a seprate score at all, but a timer that increases every tick, and represents how long someone has been playing your game. There are lots of ways to implement a scoring system, and which one you choose will depend on the specific mechanics of your individual game.
Now your scoring system is in place, but how will the person playing your game know what their score is? You’ll want to display the score on the screen.
Which function handles how the game state is drawn?
In the draw-state function, images are placed onto the background using put-image to draw the game. But the score is represented by a Number: we need a way to represent it as an Image. Thankfully, Pyret has some built-in functions that can help with this: the function num-to-string takes in a Number for its domain and returns a String representation of that number. This string can then be passed to the text function to return an Image that can be used in draw-state.
Copy the following contracts into your workbook:
-
# num-to-string :: Number -> String -
# text :: String, Number, String -> Image -
How would you use the
num-to-stringandtextfunctions together to draw the score into the game? -
How do you get the
scoreout of the game state? -
How large should the text of the score be? Where should it be placed on your game scene?
The expression:
put-image(text(num-to-string(g.score), 20, "white"), 320, 240, BACKGROUND-IMG)will place the score (drawn in size 20 white text) onto the center of the BACKGROUND-IMG.
Use these functions to draw the score onto your game screen. You could also use the string-append function to make it clear to players that the number they see is their score, like so:
text(string-append("Score: ", num-to-string(g.score)), 20, "white")These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Adding Levels
Adding Levels
Students parameterize other parts of their game, so that the experience changes as the score increases. This track delves deeper into conditionals and abstraction, offering students a chance to customize their games further while applying those concepts.
Product Outcomes |
|
|||||||||||||||
Materials |
||||||||||||||||
Language Table |
|
- helper function
-
a small function that handles a specific part of another computation, and gets called from other functions
Adding Levels 45 minutes
Overview
This activity introduces a programming pattern to add levels to students' games. For now, the only thing a level does is change the background - but students can easily extend this to change other aspects of the game.
Launch
You can add depth to your game by adding levels. In this lesson, we’ll cover making new levels based on the game’s score. To start, we want our Ninja Cat game to have a different background image when the player progresses to the next level. We’ll say that the player reaches level two when his or her score is greater than 250.
Where do you define the BACKGROUND-IMG image in your game? Keep your original background for the first level, but define a new variable, BACKGROUND2-IMG, that will be used for level 2. For the best results, use an image that is the same size as your original background.
Once you have your second background image, it should be drawn into the game — but only when a certain condition is met. Think back to the helper function we wrote to change the color of the sunset animation in Unit 4, and we need to do the same thing here!
-
What must be true for the player to progress to level 2?
-
Write a function draw-bg, which consumes the score and produces the appropriate background image.
Now that we have our helper function, we can use it to draw of that one part of the animation. Instead of blindly putting BACKGROUND-IMG into our function, now we’ll use draw-bg(g.score):
fun draw-state(g):
put-image(text(
string-append("NinjaCat! Score: ", num-to-string(g.score)),
20, "white"),
310, 470,
put-image(
text("Use arrow keys to move. Jump on the dog & catch the ruby!",
12, "white"),
320, 450,
put-image(PLAYER-IMG, g.playerx, g.playery,
put-image(CLOUD-IMG, 150, 350,
put-image(RUBY-IMG, g.targetx, g.targety,
put-image(DOG-IMG, g.dangerx, g.dangery,
draw-bg(g.score)))))))
...Investigate
Now our Ninja Cat game has a level 2! You can add more conditions to draw-bg to have multiple levels. You can use this same technique in lots of ways:
-
Write
draw-playerand changedraw-stateso that have the Player transform if the score is above 250. -
Change your animation functions so that your characters move faster if the score is above 250.
-
Add a special key (jumping? firing? warping?) that is only unlocked if the score is above 250.
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Making Pong
Making Pong
Students use the Animation Design Worksheet to decompose a 2-player game of Pong, and implement it as a Reactor-based program.
Product Outcomes |
|
|||||||||||||||
Materials |
|
|||||||||||||||
Language Table |
|
|||||||||||||||
Preparation |
Setting up the Paddles 45 minutes
Overview
Students decompose a complex problem (implementing Pong) into simpler sub-problems, and implement the paddle portion of the game.
Launch
In Unit 3, you practiced decomposing simple animations into their data structures and functions. Let’s consider how a 2-player game of Pong works: There are two "players", each represented by a paddle on either side of the screen. Each paddle can move up and down, as long as they remain on the screen. There is also a ping-pong ball, which moves at any angle and can be on or off the screen. Let’s start out by adding the paddles, making sure they can move up and down, and then we’ll add the ball later.
Using a blank Animation Design Worksheet, figure out how the paddles behave throughout the game, and decide what Data Structure you’ll need to represent those behaviors.
Students should realize that each paddle is simply a y-coordinate, since neither paddle can ever move left or right.
Here is one possible structure that we could use to model the two players:
# a PongState has the y-coordinate
# of paddle1 and paddle2
# (no x-coordinate needed, since
# the paddles only go up/down!)
data pongState:
| pong(
paddle1Y :: Number,
paddle2Y :: Number)
endWe can imagine a few sample PongState instances, in which the paddles are at different locations on the screen. If you haven’t already, it would be a good idea to define a sample state for when the game starts, and maybe two other states where the paddles are at other locations.
We’ll need to answer some questions, in order to write our draw-state function.
-
What will the paddles look like?
-
What does the background look like?
-
How wide is the background? How tall is it?
-
Define the function draw-state, and try drawing your sample PongState instances to make sure they look the way you expect them to.
The paddles don’t move on their own, so right now there’s no next-state-tick function. However, they DO move when a user hits a key! That means we’ll need to define next-state-key, and answer a few questions in the process:
Investigate
-
What key makes
paddle1Yincrease? Decrease? -
What key makes
paddle2Yincrease? Decrease? -
How much does each paddle move when it goes up or down?
-
What happens if some other key is pressed?
-
Use the Design Recipe to write the code for
next-state-key
Have students discuss their answers to these questions, before moving on to next-state-key.
At this point, we know how to change the PongState in response to a keypress and how to draw that PongState as an image. Let’s build a reactor, which uses a PongState instance as the starting state and hooks up these functions to the on-key and to-draw event handlers.
pong-react = reactor:
init: pongState(200, 200),
on-key: next-state-key,
to-draw: draw-state
endWhen you run this reactor with interact(pong-react), you should see your initial instance drawn on the screen, and the paddle positions should change based on the keys you press! Do all four keys do what you expect them to do? What happens if you hit some other key?
Right now, what happens if you keep moving one of the paddles up or down? Will it go off the edge of the screen? We should prevent that!
Take a few minutes and discuss with your partner: what needs to change to stop the paddles from going offscreen? You can use an Animation Design Worksheet if you want to be precise. Once you have a strategy that you feel confident about, take 15 minutes to try it out!
Synthesize
Give the class 2-3 minutes to discuss, and then have different teams share back before they start to implement.
Adding the Ball 45 minutes
Overview
Students modify the game State to add a ball, which can move in two dimensions.
Launch
Now that we’ve got our paddles set up, it’s time to start thinking about the ball. What do you notice about the ball? Have students volunteer lots of observations, and write them on the board. Only add the questions below to spark discussion if students run out of ideas:
-
When does the ball move? On its own, or only when a key is pressed?
-
Does the ball’s position change? If so, by how much?
-
What do we need, to keep track of the ball’s position?
-
Does the ball’s direction change?
-
What do we need, to keep track of the ball’s direction?
-
When does the ball’s direction change?
Investigate
Use an Animation Design Worksheet to add one part of the ball’s behavior to your game.
- Did your
PongStatechange as a result? Chances are, you needed to add `ballX -
Number` and
ballY :: Numberfields to your State, to make sure the ball could move in any direction. Did yourdraw-statefunction need to change? What aboutnext-state-key? Did you need to writenext-state-tick? If so, what did you do?
Some students will hard-code numbers for moving the ball. That’s okay! Once they start thinking about changing direction, those numbers will have to become fields in pongState, which change in response to paddle collisions.
Now the game is starting to come together! We’ve got two paddles moving up and down, and we make sure they stay on the screen. Meanwhile, we have a ball that can move in any direction…but so far the ball doesn’t know how to bounce! It’s time to plan out what bouncing will look like, and wire it all together.
-
How do you know when the ball has hit the top or bottom wall of the screen?
-
Write
is-on-wall, using the Design Recipe to help you.
The goal of this activity is to have students get their collision-detection working, in preparation for the bouncing behavior.
-
When a ball is moving up and to the right, what is happening to ballX and ballY?
-
When that ball hits a wall, what should happen?
-
How does the ball’s direction change after it hits a wall?
-
After it’s changed direction, how does the ball’s position change?
-
Use the Animation Design Worksheet to plan out the bouncing behavior
Watch out! This activity is pretty sophisticated! You’ll want to make sure there are plenty of visual scaffolds for students, or (even better!) have them generate these diagrams themselves. |
By now, you may have noticed that the direction of the ball itself needs to change, which means it needs to be added to our PongState structure. There are lots of different ways we could represent direction: it could be a String (e.g. “north”, “southeast”, “west”, etc), or it could be a pair of Numbers that represent how much the ball is moving in the x- and y-direction from frame to frame.
What other ways could you represent direction? What are the pros and cons of each representation?
Here is one example of a way to represent this, during Numbers to keep track of direction:
# a PongState has the y-coordinates
# of paddle1 and paddle2,
# x and y-coordinates of the ball,
# and x and y-coordinates
# representing the direction of the ball
data pongState:
| pong(
paddle1Y :: Number,
paddle2Y :: Number,
ballX :: Number,
ballY :: Number,
moveX :: Number,
moveY :: Number)
endWhen the game begins, we can start out with moveX and moveY being specific numbers that move the ball up and to the right. We can change these later, or even make them randomized every time the game starts!
Before we worry about the paddles, let’s start by thinking about the top and bottom walls of the game screen.
-
What should happen if the ball hits the top of bottom of the screen?
-
How would you detect a collision with the top or bottom wall?
-
Make the ball bounce off the top and bottom, using the Animation Design Worksheet and the Design Recipe to help you if you get stuck!
Now let’s make some sample instances for when the game begins, when the ball is about to hit a paddle, and then immediately after:
# an instance where the paddles are
# at the starting position,
# the ball is in the center (300, 200),
# and moving to the right by 20
# and up by 10 on each tick
pongStateA = pong(200, 200, 300, 200, 20, 10)
# an instance where the ball (x=150, y=280)
# is about to hit the top wall
pongStateB = pong(200, 300, 150, 280, 20, 10)
# an instance after the ball (x=550, y=280)
# hits the top wall
# it's still moving right (20),
# but now it's moving down instead of up (-10)
pongStateC = pong(200, 300, 550, 320, 20, -10)The ball starts out moving up and to the right, but once it hits a wall the direction needs to change. Instead of moving up (adding 10 each tick), it’s now moving down (adding -10 each tick) after bouncing off the wall (it’s still moving up the screen by 10 each time, so we leave that unchanged). Note: Once the ball hits the wall, its y-position needs to change! If the ball stays where it is, it will still be considered to have "hit" the wall on the next tick. This will cause the ball to jitter back and forth, as it constantly hits the same wall over and over.
Change next-state-tick so that it generates the next PongState using the ball’s previous position and the move fields. Then, add conditionals to next-state-tick so that it will change the direction of the ball when it’s hit a walll
Let’s walk through our new next-state-tick function, and make sure we understand it:
# next-state-tick :: pongState -> pongState
# move the ball, based on direction fields
fun next-state-tick(w):
if (is-on-wall(w)):
pong(
w.paddle1Y,
w.paddle2Y,
# the paddles don't change position
w.ballX + w.moveX,
# the ball keeps moving in the same x-direction
w.ballY + (w.moveY * -1),
# but it bounces off the wall (move backwards by moveY)
w.moveX,
# the x-direction stays the same
w.moveY * -1)
# and the y-direction is reversed
else:
pong(
w.paddle1Y,
w.paddle2Y,
w.ballX + w.moveX,
w.ballY + w.moveY,
w.moveX,
w.moveY)
end
endIf a collision with an upper or lower wall occurs, we need to do two things. First, we need to move the ball to it’s next position, and make sure that new position is far enough away from the paddle so that it won’t be considered another collision. Second, we need to flip the y-direction so that the ball is moving in the opposite direction. This is easy to do, by multiplying the moveY by −1.
Now it’s time to start thinking about a different kind of collision: what happens when the ball hits a paddle?
-
How do you know when the ball has hit
paddle1?paddle2? -
Write
hit-paddle1andhit-paddle2, using the Design Recipe to help you. -
Change
next-state-tickso it checks for a paddle collision in addition to the wall collision.
Closing 5 minutes
You’ve got the beginnings of a very nice Pong game! What are some features you might want to add?
Let students brainstorm ideas. Some suggestions: keeping score, a game-over event, a splash screen…
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Going Deeper: Nested Structures
Going Deeper: Nested Structures
Students refactor code from a simple animation to include structures within structures, and see how to use nested structures in their own games and animations to manage complexity.
Product Outcomes |
|
|||||||||||||||
Materials |
||||||||||||||||
Language Table |
|
|||||||||||||||
Preparation |
|
- helper function
-
a small function that handles a specific part of another computation, and gets called from other functions
Nested Structures: Managing Complexity 45 minutes
Overview
Students are introduced to the need for nested data structures, as a way of managing complexity.
Launch
Now that you know all about data structures, you’re able to use them to make video games and animations from scratch, including games that are much more complex than those you worked on in Bootstrap:Algebra. However, as you add more things to your game, you quickly end up with a large number of elements in your data structure. (If you have multiple characters in your game, each with their own position, speed, costume, etc. that all change, your structure can become quite long and unwieldy.)
Making changes to your structure, or writing functions to alter it, can get extremely complex. One way to manage this complexity is to use nested structures: Just like we can write functions to handle repetitive processes, we can make structures to handle repetitive data. For example, if each of our 4 game characters have their own x and y coordinates, we could make one Position structure to use for each character. Then, instead of our game structure containing 8 numbers, it only contains 4 Positions.
Let’s start out with a small animation to explore the benefits of nested structures. Open the Pinwheels Starter #1 file in Pyret, and click "Run". We see four colorful pinwheels spinning in the breeze. Now, take a look at the code:
# A PinwheelState is the angle of rotation for 4 pinwheels
data PinwheelState:
| pinwheel(
p1a :: Number,
p2a :: Number,
p3a :: Number,
p4a :: Number)
end
STARTING-PINWHEELS = pinwheel(60, 3, 25, 70)The only things that change in this animation are the angles of rotaton for each of the 4 pinwheels, and each of those numbers are included in the PinwheelState data structure. As usual, we have a next-state-tick function to handle updating the state of the animation, and a draw-state function to draw the animation. We also have two helper functions to do some of the work for these main functions: update-pinwheel, which increases the angle for an individual pinwheel, and draw-pinwheel, which rotates the pinwheel image by the given angle. We’ll talk about helper functions in greater detail later, but for now, notice that because we’ve delegated most of the heavy lifting to these helpers, our next-state-tick function only needs to make a new PinwheelState by calling on update-pinwheel to increase the angle of rotation for each number in the structure. Most of the actual work in this function is done by update-pinwheel.
Suppose we wanted each of the pinwheels to spin at a different speed. We already know that any changeable part of the animation will need to be added to the structure, so we’ll need to add 4 new numbers to the PinwheelState structure.
Investigate
Print out the following link: code screenshot from the pinwheels file and underline or highlight each spot in the code you would need to change in order to add a speed to each pinwheel. Once you’ve identified which sections of the code will need to change, edit the program on the computer so that each pinwheel spins at a different speed.
Now we have a nice animation of pinwheels spinning at different speeds, but what if we had started off by making each individual pinwheel its own structure? As we’ll see shortly, this can help save us some time and headaches down the road, if we want to add to our animation later.
Open the Pinwheels Starter #2 file on your computer and take a look at the code. What differences do you see between this starter file and the first?
This animation looks exactly the same, but the data structure and the code is slightly different. This time, the PinwheelState data structure contains four Pinwheels, each their own structure, instead of four numbers. The angle of rotation is now contained inside the Pinwheel structure:
# A Pinwheel is an angle of rotation
data Pinwheel:
| pw(angle :: Number)
end
# A PinwheelState is 4 Pinwheels
data PinwheelState:
| pinwheels(
p1 :: Pinwheel,
p2 :: Pinwheel,
p3 :: Pinwheel,
p4 :: Pinwheel)
end
STARTING-PINWHEELS = pinwheels(pw(60), pw(3), pw(25), pw(70))-
How would you get
pw1out of theSTARTING-PINWHEELSinstance? -
How would you get the angle out of
pw2in theSTARTING-PINWHEELSinstance?
With nested structures, accessing fields in the "child" structure (in this case, Pinwheel requires two dots. So, STARTING-PINWHEELS.pw1 produces pw(60), the first Pinwheel. Whereas STARTING-PINWHEELS.pw2.angle produces 3, the angle of pw2.
Another change between the non-nested and nested versions of the code is that in the nested version, our helper functions update-pinwheel and draw-pinwheel now take in a Pinwheel data structure, as opposed to just a number. The animation still works and looks the same on the outside, and the code hasn’t changed too drastically.
Let’s do the same activity for the nested version of the code, where we make each pinwheel spin at a different speed.
Print out the following code screenshot for the nested pinwheels file, and underline or highlight each spot in the code you would need to change in order to change each pinwheel’s speed independently. Once you’ve identified which sections will need to change, edit the nested version of the program on the computer.
Point out the differences in underlining between the two code screenshots. Note that when students finish this activity, both of the animations will look the same- but one program will have been much more straightforward to modify! We wrote a bit more code at the beginning to set up the nested structures, but that paid off later by giving us more flexibility to change the behavior of the pinwheels.
Just by looking at the differences on paper, we can see the difference in complexity of changing our animations. In order to make each pinwheel spin at a different speed, much more of the non-nested program will need to change, as opposed to the nested version where only the Pinwheel structure, STARTING-PINWHEELS instance, and the update-pinwheel function need to be edited.
What if we wanted to add a breeze to our animation, and make the pinwheels move across the screen to the left? Let’s assume that each pinwheel moves at the same speed, but each of their x-coordinates will need to change.
Go through the same process as before: Starting with the non-nested version of the code, print out these code screenshots:
-
Non-nested pinwheels
and underline or highlight the places in the code you would need to edit in order to change the x-coordinates of each pinwheel. Do this for both the nested and non-nested versions of the animation.
As before, we end up underlining, and needing to change much more of the code in the non-nested version of the animation. We also may realize something important about the non-nested code: if both a pinwheel’s angle of rotation and its x-coordinate are changing, we’re no longer able to use our update-pinwheel helper function. Previously, this function consumed an angle and speed, and added these numbers together to produce the new angle. However, since functions can only return one thing at a time, we can’t use this function to produce the updated angle and updated x-coordinate. Instead, the work of decreasing the x-coordinate must be done inside next-state-tick. Writing that code is nothing new, but wouldn’t it be nice to leave next-state-tick alone, and update each pinwheel individually inside the helper function?
Synthesize
Compare the updating functions for the non-nested version of the code:
# update-pinwheel :: Number, Number -> Number
fun update-pinwheel(angle, speed):
angle + speed
end
# next-state-tick :: PinwheelState -> PinwheelState
fun next-state-tick(ps):
pinwheel(
update-pinwheel(ps.p1a, ps.p1speed),
ps.p1speed,
ps.p1x - 5,
update-pinwheel(ps.p2a, ps.p2speed),
ps.p2speed,
ps.p2x - 5,
update-pinwheel(ps.p3a, ps.p3speed),
ps.p3speed,
ps.p3x - 5,
update-pinwheel(ps.p4a, ps.p4speed),
ps.p4speed,
ps.p4x - 5)
end
And the nested version:
# update-pinwheel :: Pinwheel -> Pinwheel
fun update-pinwheel(p):
pw(p.angle + p.speed, p.speed, p.x - 5)
end
# next-state-tick :: PinwheelState -> PinwheelState
fun next-state-tick(ps):
pinwheels(
update-pinwheel(ps.p1),
update-pinwheel(ps.p2),
update-pinwheel(ps.p3),
update-pinwheel(ps.p4))
endNot only is the version which uses nested structures much shorter, it’s also much more readable. Using a nested structure affords us a unique opportunity for abstraction. If each pinwheel moves the same way, we can use one helper function on all of them, each time consuming a pinwheel and producing the updated pinwheel. This way the only function that needs to change is the one which addresses the "child" structure (in this case, update-pinwheel, which consumes a Pinwheel), and the function next-state-tick, which consumes the "parent" structure PinwheelState, can stay unchanged. This offers you lots more flexibility when making changes to your code, or adding things to a program.
You’ve seen how nested structures work inside a simple animation, but what about a more complex video game? Let’s return to he Ninja Cat game from Bootstrap:Algebra. Here’s the original data block and some sample instances from Ninja Cat:
# A GameState is a Player's x and y-coordinate, danger's x and y coordinate and speed, and target's x and y coordinate and speed
data GameState:
game(
playerx :: Number,
playery :: Number,
dangerx :: Number,
dangery :: Number,
dangerspeed :: Number,
targetx :: Number,
targety :: Number,
targetspeed :: Number,
score :: Number)
end
# Some sample GameStates
START = game(320, 100, 600, 75, 5, 1500, 250, 10, 0)
PLAY = game(320, 100, 600, 75, 5, 300, 250, 20, 0)And here’s the same game made with nested structures. To clean up the GameState structure, make it easier to read, and allow more flexibility in our code, we defined a new structure to represent a Character, which contains a single set of x and y-coordinates:
# A Character is an x and y-coordinate
data Character:
char(
x :: Number,
y :: Number)
end
data GameState:
game(
player :: Character,
danger :: Character,
dangerspeed :: Number,
target :: Character,
targetspeed :: Number,
score :: Number)
end
# Some sample GameStates
START = game(char(320, 100), char(600, 75), 5, char(1500, 250), 10, 0)
PLAY = game(char(320, 100), char(600, 75), 5, char(300, 250), 20, 0)For the nested structures version of Ninja Cat:
-
How would you get the player’s x-coordinate out of START?
-
What about the danger’s y-coordinate?
-
How would you get the target’s speed out of PLAY?
-
Finally, what do you notice about these two versions of the Ninja Cat data? Which do you prefer, and why?
Have students discuss the pros and cons of writing a game using nested or non-nested structures.
Now take a look at YOUR video games. If you were to re-write your program to use nested structures, what would it look like? Do you have multiple characters in your game with their own x, y, and speed? Do you have any opportunities to use helper functions to move characters in the same way?
For practice, re-write the data block and sample instances for your video game using nested structures.
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Feature: Timers
Feature: Timers
Students parameterize other parts of their game, so that the experience changes as a new data field, a timer, changes. This track delves deeper into conditionals and abstraction, offering students two possible uses for a timer feature, and a chance to customize their games further while applying those concepts.
Product Outcomes |
|
|||||||||||||||
Materials |
||||||||||||||||
Language Table |
|
|||||||||||||||
Preparation |
The Watermelon Smash Starter file preloaded on students’ machines |
- constructor
-
a function that creates instances of a data structure
Adding a Splash Screen 30 minutes
Overview
One of the simplest uses for a timer is a splash screen: something that is shown for a few seconds when you first run a game. Students implement a splash screen for their games, as a way of getting comfortable with the idea of passing a timer into their Reactor.
Launch
Timers are a key component in many video games: players may need to reach a certain objective before time runs out, or keep from losing a game for longer and longer periods of time to reach a high score. In this feature, we’ll cover two possible uses of a timer in your game: adding a “splash screen” at the beginning to give instructions to the player, and adding a short animation when two characters collide.
Of course, a timer is a piece of data in our game that will be changing, meaning it should be added to our data structure. We’ll be adding a timer to the completed Moving Character file from Unit 5, and you can follow along using the same file, or your own video game project.
Investigate
Add a field called “timer” to the data structure, represented by a Number. Then, go through your code and add that field to each constructor call in your code. Once complete, run your program to make sure there are no errors, then move on.
The next step is to find (or make!) the image you want displayed as your splash screen when the game begins. We’ve made a simple image of instructional text overlayed onto the background, and defined it using the name instructions.
instructions = overlay(text("Press the arrow keys to move!", 50, "purple"),
rectangle(640, 480, "solid", "white"))Encourage students to get creative here: In addition to giving instructions to a user, they can also use their splash screen to provide a backstory for their game, include names and images of their characters, and of course, note who created the game!
As of now, our Moving Character file doesn’t have a next-state-tick function, but if we want our timer to increase or decrease, we’ll have to add one. If you already have a next-state-tick function with the timer added to the State it produces, make it so the timer increases by 1 on every tick. Don’t forget to add on-tick: next-state-tick to the reactor once you finish! Our next-state-tick function looks like this:
# next-state-tick :: CharState -> CharState
fun next-state-tick(a-char):
char(a-char.x, a-char.y, a-char.timer + 1)
end(Note that the position of the character doesn’t change in next-state-tick. It only changes in response to keypresses, which is already handled in the next-state-key function.)
Now we have a timer added to our CharState structure, and it increases as the reactor runs. But how do we display our instructions screen based on the timer? The draw-state function handles how the game looks, so we’ll have to add some code to this function. In our starting CharState, which we named middle, we had the timer start at 0: middle = char(320, 240, 0). Since we made the timer increase by 1 every clock tick, we’ll display the instructions image as long as the timer is 100 or below.
By default, the computer’s clock ticks 28 times each second, so the instructions screen will be up for a bit less than 4 seconds.
We’ll need to change draw-state so that it becomes a piecewise function. If the given CharState’s timer is less than or equal to 100, (the very beginning of the game) our splash screen should be displayed. Otherwise, the image of Sam the butterfly should be displayed at the correct position on the background, which is what the current code already does. To change draw-state, we add one new if: branch, and add the original code to the else: clause.
# draw-state :: CharState -> Image
fun draw-state(a-char):
if a-char.timer <= 100:
instructions
else:
put-image(sam, a-char.x, a-char.y, rectangle(640, 480, "solid", "white"))
end
endSynthesize
Have students explain what’s going on in their own words. (We only want the splash screen to appear at the very start of the game, when the timer is below a certain amount. All other times, we should see the game itself.)
Click "Run", and test out your new feature! You may want to increase or decrease the amount of time your splash screen is displayed, or make changes to the image itself.
Following these steps, students should end up with something similar to this completed Moving Character file.
Timer-Based Animations 45 minutes
Overview
Students implement a timer-based animation, to create a temporary effect when a collision occurs.
Launch
Another way to use timers in a game is to add a short animation when a collision occurs. In this example, we’re going to add a timer to a simple animation, but you could extend this to add an animation to your game when two characters collide, when the player reaches a goal, etc.
Note that if students have already used a timer to add a splash screen to their game, they will not be able to use the same timer field to display a collision animation. Instead, they could implement a collision animation in a different game, or add another, seprate field to their data structure: animation-timer and instruction-timer, for instance.
Open the Watermelon Smash Starter file and click "Run".
Our goal is to make a complete animation of a watermelon getting smashed by a mallet. When the mallet reaches the melon, we should see some sort of pink explosion! We’ve gotten you started by including a data structure called SmashState, which contains the y-coordinate of a mallet and a timer. When the reactor begins, the initial state (defined here as START) defines the mallet at 250 and the timer at 0.
To start, let’s look at the draw-state function.
# draw-state :: SmashState -> Image
# draws the image of the watermelon and mallet on the screen.
fun draw-state(a-smash):
put-image(MALLET, 275, a-smash.mallety,
put-image(WATERMELON, 200, 75, BACKGROUND))
endCurrently, this function uses the images we’ve defined above (WATERMELON, MALLET, etc.) and draws the image of the mallet at x-coordinate 275 and the given SmashState’s current mallety, on top of the image of the watermelon, placed at the coordinates 200, 75 on the background. This code works for most of the animation, before the mallet hits the watermelon, but we want to see a pulpy explosion once it does.
-
When should we see a watermelon pulp explosion in this animation? What must be true about the given
SmashState? -
Which image should we replace to show the explosion animation? The mallet, or the watermelon?
Once the mallet reaches the watermelon (around y-coordinate 140), we should replace the watermelon image with one representing an explosion. Here, we’ll use a radial star, whose contract is written below:
# radial-star :: Number, Number, Number, String, String -> ImagePractice making a few radial stars of different colrs and sizes in the interactions area. See if you can determine what each of the Number arguments represent.
Most importantly for our purposes, the second argument to radial-star represents the outer size of the star. Since we want this star to represent the exploding watermelon, and grow larger as the animation progresses, we can’t use a static number for the size. Instead, we want to use one of our changing values from the SmashState.
Which field should we use to represent the size of the growing explosion? mallety, or timer? Why?
mallety only represents the y-coordinate of the falling mallet, whereas the timer can be set and reset based on certain conditions to represent the changing size of the star image.
Investigate
Change the draw-state function to make it piecewise: when the mallet’s y-coordinate is 140 or less, draw the following image of the radial star (radial-star(20, a-smash.timer, 25, "solid", "deep-pink")) at the watermelon’s current coordinates. In all other cases, produce the current body of draw-state.
The updated draw-state function should look similar to:
# draw-state :: SmashState -> Image
# draws the image of the watermelon and mallet on the screen. When the
# mallet's y-coordinate reaches 140, draw the explosion
fun draw-state(a-smash):
if (a-smash.mallety <= 140):
put-image(radial-star(20, a-smash.timer, 25, "solid", "deep-pink"), 200, 75,
BACKGROUND)
else:
put-image(MALLET, 275, a-smash.mallety,
put-image(WATERMELON, 200, 75, BACKGROUND))
end
endNote to students that we haven’t done anything to change the value of a-state.timer yet! If the timer’s value is still 0, as it begins in our START state, we won’t see any star at all, even if our code is correct. We’ll work on changing the value of the timer in response to different conditions within the next-state-tick function.
Now take a look at the next-state-tick function defined below.
# next-state-tick :: SmashState -> SmashState
# Decreases the y-coordinate of the mallet every tick
fun next-state-tick(a-smash):
smash(a-smash.mallety - 2, a-smash.timer)
endCurrently, this function decreases the mallet’s y-coordinate to make it fall, and doesn’t change the timer. However, if we want the size of our explosion to increase, at some point we’ll have to start increasing the timer (since the timer’s value also represents the size of our explosion animation).
When should we start increasing the timer, thereby increasing the size of the watermelon’s explosion animation?
For help, we can look back at our draw-state function. We only wanted to start drawing the explosion (the pink radial star) when mallety was less than or equal to 140. So we can check the same condition in next-state-tick to tell us when to start increasing the SmashState’s timer.
Turn next-state-tick into a piecewise function: once a-smash.mallety reaches 140 or less, continue decreasing it’s y-coordinate, but also increase the timer by 2. Use the original body of next-state-tick as your else clause.
The final version of next-state-tick should look similar to:
fun next-state-tick(a-smash):
if (a-smash.mallety <= 140):
smash(a-smash.mallety - 2, a-smash.timer + 2)
else: smash(a-smash.mallety - 2, a-smash.timer)
end
endRun your program, and watch that watermelon get smashed!
For a challenge, change the draw-state function so that once the mallet has passed below a certain threshold, an image of the smashed watermelon (we’ve defined one called SMASHED) appears. Hint: Where within the draw-state function will this new condition need to be placed in order for it to work properly?
Closing
We’ve shown you a couple ways to use timers in your games and animations, but there are many more possibilities. You could extend the timer animation to add a short animation when two characters have collided, or display an ever-increasing timer on the screen to show players how long they have ben playing your game. What other uses for timers can you come up with?
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598).  Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap:Reactive by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.